Le rette tangenti condotte da un punto P ad una circonferenza possono essere o due o una sola a seconda se il punto P è estern

Le rette tangenti condotte da un punto P ad una circonferenza possono essere o due o una sola a seconda se il punto P è esterno o appartiene alla circonferenza:

Il problema della determinazione delle rette tangenti condotte da un punto qualsiasi ad una circonferenza ma anche ad un’altra qualsiasi conica (parabola, ellisse, iperbole) si risolve applicando il seguente:

METODO GENERALE: (valido per qualsiasi conica)

si verifica dapprima se il punto P appartiene alla circonferenza
se vi appartiene allora da quel punto si può condurre una ed una sola retta tangente alla circonferenza
se non vi appartiene, ossia P è esterno, allora esistono due rette tangenti alla circonferenza

1. si scrive l’equazione della generica retta passante per un punto noto P(x₁; y₁):

y – y₁ = m ( x – x₁)

2. si imposta il sistema fra le equazioni della circonferenza e della generica retta:

3. per sostituzione si ottiene l’equazione risolvente il sistema di 2° grado

4. si pone ∆ = 0 (condizione di tangenza) affinché la retta diventi tangente alla circonferenza

5. si risolve l’equazione così ottenuta nell’incognita m e indicate con m₁ e m₂le soluzioni si hanno i seguenti due casi:

§ m₁ ≠ m_{2 ,}cioè esistono due rette tangenti, quando il punto P è esterno alla circonferenza

§ m₁ = m₂, cioè esiste una sola retta tangente, quando P appartiene alla circonferenza

6. si sostituisce la soluzione o le soluzioni trovate nell’equazione della generica retta

Però rispetto ad altre coniche il problema della determinazione delle tangenti ad una circonferenza può essere risolto mediante altri procedimenti che sono caratteristici della circonferenza e che per questo sono detti:

METODI PARTICOLARI: (validi solo per la circonferenza)

1. Procedimento risolutivo che si basa sulla proprietà, vedi fig.1 e fig.2, che le tangenti alla circonferenza condotte da un punto P qualsiasi hanno dal centro distanza uguale al raggio della circonferenza

si determinano le coordinate del centro C e il raggio r della circonferenza

si scrive l’equazione della generica retta y – y₁ = m( x – x₁) passante per il punto P(x_1;y₁) in forma implicita

si applica la formula della distanza del centro C dalla retta generica imponendo che sia uguale al raggio

§ si ottiene così un’equazione di 2° grado nell’incognita m, le cui soluzioni distinti (se il punto è esterno alla circonferenza) o coincidenti (se il punto appartiene alla circonferenza) sostituiti nell’equazione generica della retta determinano le tangenti

2. Procedimento risolutivo (solo se il punto appartiene alla circonferenza) che si basa sulla proprietà, vedi fig.2, che la tangente t alla circonferenza in un suo punto P è perpendicolare alla retta PC:

si scrive l’equazione generica della retta per P: y – y₁ = m_t ( x – x₁)
si determinano le coordinate del centro C della circonferenza
si calcola il coefficiente angolare m_PC della retta passante per P e C
si impone che m_t sia l’antireciproco di m_PC
si sostituisce il valore di m_t nell’equazione generica per P

Risolviamo adesso problemi relativi alle tangenti utilizzando però i metodi particolari che sono più semplici dal punto di vista dei calcoli da svolgere.

1. Problema

Determinare le equazioni delle rette tangenti alla circonferenza x ² + y ² + 4 x – 2 y –15 = 0 passanti per il punto P( 4; -1)

Verifichiamo dapprima se P appartiene alla circonferenza imponendo la condizione di appartenenza di un punto ad una curva:

(4) ² + (-1) ² + 4 ^. (4) – 2 ^. (-1) –15 = 0 → 16 +1 + 16 +2 -15 = 0 → 20 ≠ 0

quindi il punto P è esterno alla circonferenza (dato che se P fosse interno non si potrebbero condurre tangenti alla circonferenza bensì secanti) e pertanto da esso escono due tangenti.

Applichiamo dunque il 1. procedimento risolutivo che si basa sulla proprietà che la tangente ha dal centro della circonferenza distanza eguale al raggio; seguiamo passo passo l’algoritmo descritto:

· si determinano le coordinate del centro C e il raggio r della circonferenza

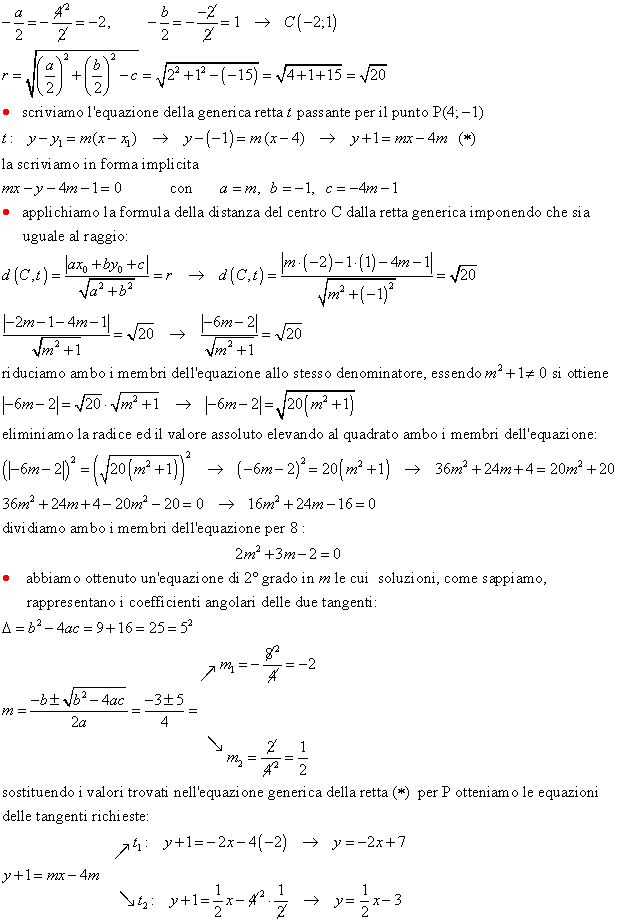
2. Problema

Determinare la retta tangente alla circonferenza: x ² + y ² + 2 x – 4 y –35 = 0, nel punto P(5;4)

Verifichiamo se P appartiene alla circonferenza:

(5) ² + (4) ² + 2 ^. (5) – 4 ^. (4) –35 = 0 → 25 + 16 + 10 – 16 – 35 = 0 → 51 – 51 = 0 → 0 = 0

quindi il punto P è sulla circonferenza e pertanto si può condurre ad essa una sola tangente per P.

E’ conveniente tra i due metodi particolari applicare il 2. procedimento risolutivo che si basa sulla proprietà che la tangente in P è la retta perpendicolare alla retta PC ( raggio); seguiamo dunque l’algoritmo descritto:

· scriviamo l’equazione generica della retta per P:

y – 4 = m_t ( x – 5)

· determiniamo le coordinate del centro C della circonferenza:

3. Problema

Scrivere l’equazione della circonferenza di centro C(-1;3) e tangente alla retta di equazione: 3x + 4y + 1 = 0

Per scrivere l’equazione della circonferenza, utilizzando la sua definizione, sono necessarie oltre le coordinate del centro la misura del raggio; quest’ultimo, avendo la tangente alla circonferenza, possiamo calcolarlo come distanza del centro C dalla retta tangente t, osserva fig.2, quindi applichiamo la formula: