MODELLI ALGEBRICI-GEOMETRICI

v Per rappresentare nel piano cartesiano  con sufficiente precisione una generica parabola con asse di simmetria parallelo alle y  e di equazione una funzione quadratica di tipo trinomia:

y = a x ² + b x + c          con  a, b, c ≠ 0

     occorre determinare i seguenti elementi:

v POSIZIONI PARTICOLARI DI PARABOLE (rappresentate da funzioni quadratiche di tipo binomia– monomia ):

      Se nell’equazione  y = a x ² + b x + c  si ha:

Ø c = 0

allora la parabola:    y = a x ² + b x   passa per l’origine

Ø b = 0

allora la parabola:   y = a x ² + c    ha l’asse di simmetria coincidente con l’asse y e il vertice V( 0; c) 

Ø b = c = 0

allora  la parabola:  y = a x ²     ha l’asse di simmetria coincidente con l’asse y e il vertice nell’origine

N.B.: Nel caso di parabole con modelli algebrici di tipo:

v  y = a x ², che interseca gli assi solo in V ≡ O(0;0)

v y = a x ² + c  con  a e c concordi (ossia o entrambi positivi o entrambi negativi) che non interseca l’asse delle x

v y = a x ² + b x + c  con  ∆ < 0 che non interseca l’asse delle x

non abbiamo quindi sufficienti elementi per poter rappresentare con una buona approssimazione tali parabole e pertanto è necessario determinare alcuni loro punti le cui coordinate si ottengono dando dei valori arbitrari alla x che sostituiti nell’equazione ci forniscono i corrispondenti valori delle y ; oppure, nel caso di parabola avente modello algebrico dell’ultimo tipo, è sufficiente individuare il simmetrico del punto d’intersezione dell’asse delle y  rispetto all’asse di simmetria.

ESERCIZI GUIDATI

Rappresentare graficamente le seguenti parabole con asse di simmetria parallelo alle y:

( funzione quadratica di tipo trinomia )

1)   y = x² – 6x + 5

· concavità: a = 1 >0 quindi la parabola volge la concavità verso l’alto

· vertice:

Abbiamo sufficienti elementi per poter rappresentare graficamente la parabola, quindi riportiamo le informazioni trovate nel piano cartesiano e tracciamo la curva:

2)     y = - x² + 4x - 4

· concavità: a = -1 < 0 quindi la parabola volge la concavità verso il basso

· vertice:

Riportiamo dunque le informazioni trovate nel piano cartesiano e per meglio rappresentare la parabola consideriamo come altro punto della parabola il simmetrico del punto A(0; - 4) rispetto all’asse di simmetria di equazione: x = 2 (ricorda che è la retta parallela all’asse delle y  passante per V ) che possiamo immediatamente individuare orientandoci graficamente una volta tracciato l’asse di simmetria:

3)     y =  x² + 2x + 4

· concavità: a = 1 >0 quindi la parabola volge la concavità verso l’alto

· vertice:

Per rappresentare la parabola, dato gli elementi insufficienti trovati, prendiamo in considerazione come un altro suo punto il simmetrico del punto A rispetto all’asse di simmetria: x =  -1:

( funzione quadratica di tipo binomia pura )

4)     y =  x² - 9

· concavità: a = 1 >0 quindi la parabola volge la concavità verso l’alto

· la parabola ha l’asse di simmetria coincidente con l’asse delle y e vertice V(0; c) → V(0; - 9)

· intersezioni con gli assi:

      dato che il vertice V è situato sull’asse y questo è l’unico punto di intersezione con tale asse     

      e quindi calcoliamo le intersezioni con l’asse x, che esisteranno dato che a e c sono discordi:

      Rappresentiamo la parabola nel piano cartesiano:

5)     y =  - x² - 5

· concavità: a = -1 <0 quindi la parabola volge la concavità verso il basso

· la parabola ha l’asse di simmetria coincidente con l’asse delle y e vertice V(0; c) → V(0; - 5)

· intersezioni con gli assi:

      dato che il vertice V è situato sull’asse y questo è l’unico punto di intersezione con tale asse; 

      inoltre, essendo a e c concordi  la parabola non interseca l’asse delle x, infatti:

Rappresentiamo graficamente la parabola:

( funzione quadratica di tipo monomia )

6)     y =  - 2x²

· concavità: a = -2 <0 quindi la parabola volge la concavità verso il basso

· la parabola ha l’asse di simmetria coincidente con l’asse delle y e vertice nell’origine V(0; 0)

· intersezioni con gli assi: il solo vertice

Per rappresentarla determiniamo due punti della parabola:

Rappresentiamo graficamente la parabola:

QUESITI A SCELTA MULTIPLA GUIDATI

Suggerimento: procedere per esclusione!

Data l’equazione della parabola indicare il modello grafico corrispondente tra quelli proposti:

1) y = 2 x²

Risposta: b)

Infatti la parabola data ha modello y = a x²  con :

§ concavità rivolta verso l’alto, essendo a = 2 >0, pertanto si esclude la a)

§ asse di simmetria coincidente con l’asse delle y , per cui si esclude la d)

§ vertice in (0;0),  per cui si esclude la c).

2) y =  - x² - 1

Risposta: c)

Infatti la parabola data ha modello y = a x² + c  (funzione quadratica di tipo binomia pura) con :

§ concavità rivolta verso il basso, essendo a = -1 < 0, per cui non possiamo ancora escludere nessun modello grafico

§ termine c ≠ 0,  per cui non passa per l’origine degli assi e pertanto si esclude la a) e la d)

§ asse di simmetria coincidente con l’asse delle y , per cui tra quelli rimasti non possiamo annullare nessun modello

§ vertice in (0;c) per cui V(0; -1), quindi essendo il vertice sull’asse negativo delle y si scarta la b) oppure essendo a e c concordi la parabola non interseca l’asse delle x.

3) y =  - x² + x

Risposta: a)

Infatti la parabola data ha modello y = a x² + x (funzione quadratica di tipo binomia spuria) con:

§ concavità rivolta verso il basso, essendo a = -1 < 0, per cui si esclude la b).

§ un ramo passante per l’origine degli assi, essendo c = 0, quindi possiamo escludere c)

§ il vertice non è coincidente con l’origine degli assi, altrimenti la sua equazione sarebbe di tipo monomia, per cui si esclude la d)

4) y =   x² – 6 x + 5

Risposta: d)

Infatti la parabola data ha modello y = a x² + b x + c (funzione quadratica di tipo trinomia) con:

§ c ≠ 0 dunque non passa per l’origine e si esclude la a)

§ b ≠ 0  quindi il vertice non è sull’asse y quindi si scarta la c)

§ a e b sono discordi quindi x_V ovvero l’ascissa del vertice è positiva quindi non può essere b)

Stabilire qual è il modello algebrico della parabola corrispondente al grafico assegnato:

1)

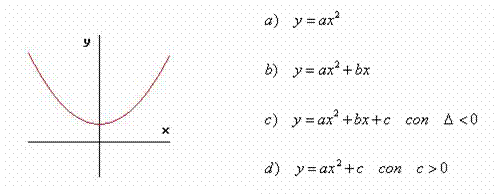Risposta: d)

Infatti il modello grafico rappresenta una parabola con :

§ asse di simmetria coincidente con l’asse y e quindi si scartano la b) e la c) che hanno asse di simmetria parallelo all’asse y ma distinto da esso

§ vertice non coincidente con l’origine degli assi e quindi si elimina la a)

2)

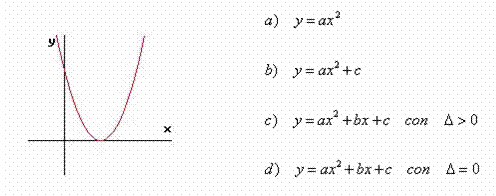Risposta: d)

Infatti il modello grafico rappresenta una parabola:

§ avente asse di simmetria parallelo e non coincidente con l’asse y, quindi si scartano la a) e la c) che hanno proprio l’asse y come asse di simmetria

§ tangente l’asse delle x in un punto coincidente con il vertice ma distinto dall’origine degli assi, quindi si tratta di una funzione quadratica di tipo trinomia con discriminante ∆ dell’equazione ad essa associata uguale a zero, di conseguenza si scarta la c).

3)

La risposta è b)

Infatti:

§ essendo la concavità rivolta verso il basso si scarta la  c)

§ poiché  c > 0  si scarta la  d), dove c = 0, e la  e), dove c < 0

§ il vertice non si trova nell’origine e pertanto si scarta la  f)

§ il vertice non si trova sull’asse delle y di conseguenza si scarta la  a).