L’integrale definito trae origine dalla risoluzione del problema delle aree, che consiste nel determinare le aree di quelle parti di piano che risultano delimitate da contorni curvilinei o mistilinei, come il trapezoide: figure, quindi, non piane di cui non è possibile calcolarne le aree utilizzando le formule della geometria piana euclidea.
Intendiamo per trapezoide T la regione di piano delimitata dalla curva della funzione y = f(x) relativo all’intervallo [a;b], ove f(x) è continua e positiva, dalle rette verticali x = a , x = b e dall’asse x, vedi fig. 1:

Come vedremo in seguito, l’area del trapezoide T sarà denominato “integrale definito della f(x) dall’estremo a all’estremo b”. Calcoliamo ora l’area di T utilizzando il metodo di esaustione: un algoritmo che Archimede applicò per calcolare l’area del cerchio, ovvero per effettuare la quadratura del cerchio. Tale metodo consiste nell’inscrivere e circoscrivere un cerchio con poligono regolari il cui numero n di lati sia sempre più elevato, vedi fig 2:

ottenendo in tal modo due successioni di aree sn dei poligoni inscritti e Sn dei poligoni circoscritti che rappresentano rispettivamente dei valori approssimati per difetto e per eccesso del cerchio A:
sn < A < Sn
Si verifica, utilizzando il concetto di limite, che le due successioni di aree {sn} e {Sn} tendono contemporaneamente allo stesso limite finito al tendere all’infinito del numero n dei lati dei poligoni inscritti e circoscritti e questo numero rappresenta l’area A del cerchio:
![]()
Adesso calcoliamo l’area del trapezoide T utilizzando il metodo di esaustione, però non ci serviremo di poligoni regolari me di particolari figure geometriche denominate plurirettangoli.
Applichiamo il metodo nel modo seguente:
§ dividiamo l’intervallo [a;b] in n parti uguali, ciascun intervallino di suddivisione avrà quindi ampiezza:
![]()
§ disegniamo i rettangoli aventi per base ∆xi e per altezza il minimo valore che la funzione assume nel corrispondente intervallino di suddivisione; infatti la funzione essendo continua, il teorema di Bolzano – Weierstrass ci garantisce l’esistenza del massimo e del minimo assoluto negli intervallini considerati;
§ indichiamo con sn la somma delle aree di tutti questi rettangoli la cui unione individua il plurirettangolo inscritto nel trapezoide:
![]()
rappresenterà, dunque, un valore approssimato per difetto dell’area del trapezoide, vedi fig. 3:
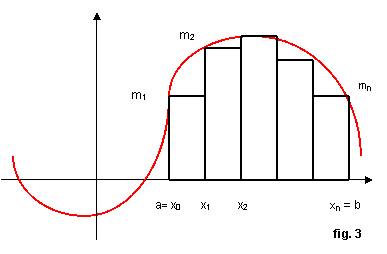
Analogamente, resta individuato il plurirettangolo circoscritto al trapezoide, costituito dall’unione delle aree, che indicheremo con Sn, dei rettangoli aventi per base ∆xi e per altezza il massimo valore che la funzione nel corrispondente intervallo di suddivisione. Evidentemente
![]()
rappresenterà un valore approssimata per eccesso dell’area del trapezoide, vedi fig. 4:
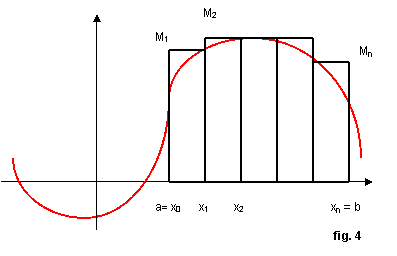
L’area del trapezoide risulta così compresa fra le due aree per difetto sn e per eccesso Sn, ossia possiamo scrivere:
sn < T < Sn
oppure
![]()
Man mano scegliamo più piccoli gli intervalli di suddivisione di [a;b] migliore risulterà l’approssimazione delle due aree.
A questo punto, facendo tendere all’infinito il numero n degli intervallino parziali di suddivisione la loro ampiezza tende a zero:
![]()
allora è intuitivo che le aree sn, ad andamento crescente, ed Sn, ad andamento decrescente, tendono a diventare uguali fra di loro, avvicinandosi indefinitamente ad uno stesso numero finito T, cioè accade che:

Pertanto :
Definizione: L’ area del trapezoide è il limite comune T a cui tendono le due successioni {sn}
e {Sn}delle aree dei plurirettangoli inscritti e circoscritti al trapezoide quando si fa
tendere all’infinito il numero n degli intervallini di suddivisione di [a;b].
Sinteticamente, utilizzando il simbolo dovuto a Leibniz, si pone:
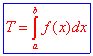
dove tale simbolo viene denominato integrale definito da a a b di f(x)dx.
Pertanto, segue per definizione che:
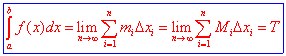
Il significato geometrico dell’integrale definito di una funzione positiva e continua in [a;b] è ovviamente l’area del trapezoide T relativo alla funzione f(x) in[a;b].
L’origine del simbolo di integrale definito non risulta evidente dalla definizione data e per renderla tale utilizziamo un altro metodo per calcolare l’area del trapezoide T, procedendo in tal modo:
§ suddividiamo [a;b] in n intervallini parziali aventi la stessa ampiezza ∆xi e consideriamo all’interno di ciascuno di essi un qualsiasi valore φi .
§ disegniamo i rettangoli aventi per base ∆xi e per altezza il valore f(φi) che la funzione assume nel corrispondente intervallino di suddivisione; infatti la funzione essendo definita e continua, il teorema di Bolzano – Weierstrass ci garantisce l’esistenza del valore che la funzione assume tra il massimo e il minimo assoluto negli intervallini considerati, vedi fig. 5;
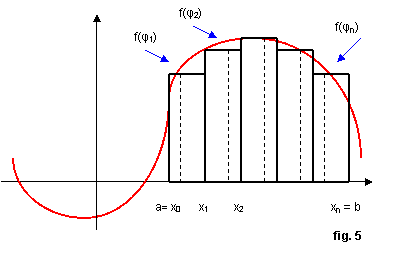
indichiamo
con σn la somma
delle aree di tutti questi rettangoli la cui unione individua il plurirettangolo
intermedio tra quello inscritto e quello circoscritto al trapezoide; l’area
σn sarà data: 
Pertanto possiamo dare la seguente
Definizione: L’integrale definito da a a b della funzione f(x) è il limite finito T a cui tende la
successione σn = ∑i f(φi)∆xi al tendere di n all’infinito.
tendere all’infinito il numero n degli intervallini di suddivisione di [a;b].
Ora appare evidente che il simbolo utilizzato da Leibniz per l’integrale definito rappresenta un’espressione sintetizzata del limite della ∑i f(φi)∆xi , per n → ∞. Infatti, il simbolo di sommatoria ∑ viene sostituito dal simbolo d’integrale ∫ , che ricorda la forma di una “ esse maiuscola ”iniziale della parola ”somma “; f(φi) viene sostituita semplicemente da f(x) con x un punto qualsiasi di [a;b] ed infine ∆xi dal differenziale dx in quanto l’integrazione definita è un’operazione di passaggio al limite per ∆xi tendente a zero (ricordiamo che il differenziale di una funzione f(x), indicato con df(x), viene definito come df(x) = f ‘(x)dx, con dx = ∆x).
Osservazioni
§ pensando l’integrale definito non come un algoritmo basato sul concetto di limite di una sommatoria bensì come un’operazione d’integrazione definita, non collegata quindi all’area del trapezoide, possiamo generalizzare il concetto di integrale definito della f(x) esteso all’intervallo [a; b] senza che essa sia in tale intervallo necessariamente continua e positiva, ossia nel caso in cui f(x) ammetta qualche punto di discontinuità e inoltre possa essere negativa in tale intervallo d’integrazione;
§ non fare confusione tra integrale definito e area: l’integrale definito della f(x) esteso all’intervallo [a;b] è il valore di un limite e quindi un qualsiasi numero reale ben determinato, l’area è sempre rappresentato invece da un numero positivo. Pertanto nel caso in cui f(x) sia positiva allora il limite è anch’esso un numero positivo e geometricamente rappresenta l’area del trapezoide relativo alla f(x) in [a;b]; nel caso in cui invece f(x) risulta negativa nell’intervallo d’integrazione tale limite sarà un numero negativo e solo il suo valore assoluto rappresenta ancora geometricamente l’area del trapezoide. Da ciò segue che l’integrale definito di una qualsiasi funzione continua, può interpretarsi come somma algebrica delle aree delle regioni di piano delimitate dalla curva f(x), dalle rette x =a, x =b e dall’asse delle ascisse, considerando negative le regioni che sono situate al di sotto dell’asse x e positive quelle situate al di sopra, vedi figura seguente:

§ differenza concettuale tra integrale definito e integrale indefinito: l’integrale definito della f esteso all’intervallo [a;b] è un numero reale ben determinato mentre l’integrale indefinito della f è un insieme di funzioni.