Una retta t  può assume tre possibili posizioni rispetto ad una circonferenza, vedi figure:

METODO GENERALE: per stabilire la posizione di una retta rispetto ad una circonferenza, si calcolano i punti di intersezione tra le due curve risolvendo il sistema tra le equazioni della circonferenza e della retta:

Quindi, per stabilire la posizione di una retta rispetto ad una circonferenza possiamo adottare due procedimenti:

1. confrontare la distanza del centro C della circonferenza dalla retta con il raggio
2. applicare il metodo generale, ovvero trovare le eventuali intersezioni, risolvendo il sistema delle equazioni delle due curve e trarre deduzioni sulla base del  discriminante dell’equazione

1. Problema

Stabilire la posizione delle seguenti rette:

1) a: x – 3 y + 13 = 0

2) b: y = 2 x – 4

3)      c: x + 2 = 0

rispetto alla circonferenza:

x ² + y ² - 2 x – 6 y + 5 = 0

e, nei casi in cui la retta non sia esterna, determinare le coordinate dei punti d’intersezione.

Applichiamo, in base alle richieste del testo, il procedimento 1. per stabilire la posizione delle rette date rispetto alla circonferenza.

1)   A tal scopo calcoliamo dapprima le coordinate del centro C e la misura del raggio r, successivamente la distanza di C dalla retta  a: x – 3 y + 13 = 0 che confronteremo con il raggio:

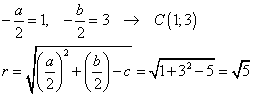
2. Problema

Determina le coordinate degli eventuali punti d’intersezione della circonferenza con la retta r nei seguenti casi: