Scriviamo l’equazione nella forma canonica:

si tratta di determinare quegli angoli x aventi una data tangente b.

Poiché, per definizione, la tangente di un angolo x rappresenta l’ordinata b del punto T d’intersezione della circonferenza goniometrica con la retta del diametro passante per T, risolvere l’equazione data significa determinare gli angoli associati ai punti della circonferenza goniometrica aventi stessa tangente b.

Utilizzando il Metodo della circonferenza e la definizione di tangente, vediamo in generale i vari passi risolutori:

1.      consideriamo dapprima l’equazione

ovvero determiniamo dapprima gli angoli x che si individuano in una sola circonferenza, cioé in un angolo giro. Il problema si risolve determinando i punti della circonferenza goniometrica aventi stessa tangente e di conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati.

2. determiniamo tali punti: disegniamo nel piano cartesiano la circonferenza  goniometrica e la retta tangente alla circonferenza nel punto A, origine degli archi. Su  tale retta riportiamo il punto T la cui ordinata è b. Tracciamo la retta del diametro passante per T; questa incontra la  circonferenza nei due punti P e P’ aventi la tangente uguale a b, vedi figure:

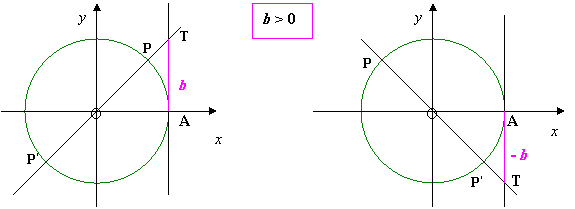
3. determiniamo gli angoli associati ai punti: partendo, al solito, dall’origine A degli archi  si individuano i due angoli AÔP e AÔP’ angoli associati ai punti P e P’aventi stessa tangente; con a il minimo angolo tale che tg x = I b I, cioè a è l’ampiezza dell’angolo positivo:

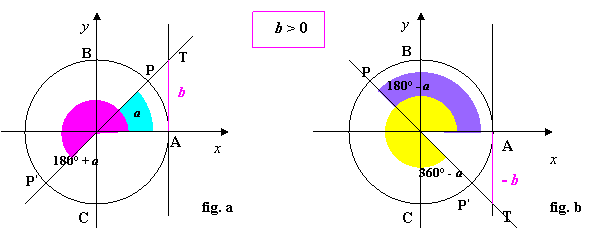
4. Le soluzioni: come si osserva in figura, i due angoli associati, soluzioni dell’equazione, che differiscono di 180° (infatti tali angoli ricordiamo hanno stessa tangente!): a e 180° - a ( fig.a) oppure 180° - a e 360° - a (fig.b) a seconda del segno di b .

In  generale, per la determinazione delle soluzioni in gradi o in radiante, si ha il seguente:

Schema  Riepilogativo

ESERCIZI SVOLTI

Risolvere le seguenti equazioni goniometriche elementari in tangente:

1)    tgx = 1           con  0° ≤ x ≤ 360°

Con l’aiuto della circonferenza goniometrica e la definizione di tangente di un angolo, ricerchiamo gli angoli x la cui tangente è 1.

Disegniamo, dunque, la circonferenza goniometrica e la retta ad essa tangente nel punto A; riportiamo sulla retta il punto T di ordinata 1. Tracciamo la retta del diametro passante per T che intersecherà la circonferenza nei due punti P e P’ ai quali corrispondono gli angoli a e 180° + a, con a = 45° essendo tg 45° =1, vedi figura :

Quindi le soluzioni dell’equazione sono:

x = 45°   e  x = 225°

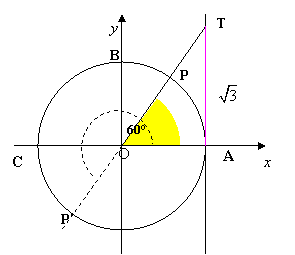
Poiché sono richieste le soluzioni in R, consideriamo, per la periodicità della funzione tangente, il solo angolo che cade in [0; 180° ] (semicirconferenza situata nel 1° e 2° quadrante) e ad esso aggiungiamo i multipli di 180° :

x = 60°  + k 180°

Le soluzioni dell’equazione in radiante sono dunque:

Da quanto detto:

affinché due angoli abbiano la stessa tangente è necessario e sufficiente che abbiano uguali gli angoli a meno di un numero intero di angoli piatti, per la periodicità della tangente:

(*)   tg α = tg β  ↔ α = β + k 180°,    α, β ≠ 90° + k 180°

Quindi se dobbiamo risolvere l’equazione seguente:

4)    tg 2 x = tg ( x + 50° )     in R

per la  (*) e per la periodicità del coseno  di 360° si scriverà:

   2 x = x +  50° + k 180°    →    2 x – x =  50° + k 180°   → x =  50° + k 180°