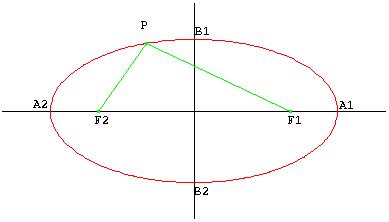
L’ellisse è il luogo geometrico dei punti del piano per i quali è costante la somma delle distanze da due punti fissi detti fuochi

Supponiamo di prendere i due fuochi sull’asse x in posizione simmetrica rispetto all’asse y (che dunque passa per il punto medio del segmento che li congiunge), ossia F₁(-c, 0) e F₂(c, 0) e  sia  P(x, y) un punto qualsiasi dell’ellisse, in base alla definizione si ha che:

( 1 )     P F₁ + P F₂ = 2a

avendo indicato con a una costante e con P F₁ e P F₂  le distanze del punto generico dai fuochi.

Sotto queste condizioni, nel piano cartesiano l’ellisse (in forma canonica)  si presenta così:

Utilizzando la definizione data dell’ellisse si perviene al suo modello algebrico: infatti, calcolate le distanze P F₁ e P F₂, utilizzando le coordinate dei punti, queste si sostituiscono nella (1) e dopo l’applicazione delle procedure risolutive per eliminare i radicali presenti  e la sostituzione di  a ² - c ² = b ²  per semplificare l’equazione si perviene alla seguente:

Equazione canonica dell’ellisse (qualunque sia l’asse in cui si trovano i due fuochi)

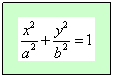
Caratteristiche:

v l’ellisse è simmetrica rispetto agli assi, detti assi di simmetria, e rispetto all’origine, detto centro di simmetria

v A₁(-a, 0), A₂(a, 0), B₁(-b, 0) e B₂(b, 0), intersezioni con gli assi, sono detti vertici dell’ellisse

v a e b  rappresentano rispettivamente le lunghezze  dei semiassi A₁O = A₂O  e  B₁O = B₂O

v i fuochi appartengono sempre al semiasse maggiore

v c è la semidistanza focale tra un fuoco e l’origine

v se  a > b   i fuochi sono sull'asse x e si avrà  c ² = a ² - b ²

v se  a < b, i fuochi sono sull'asse y  e risulta  c ² = b ² - a ²

v se la distanza focale è nulla, ovvero c = 0, allora i due fuochi coincidono nel centro dell’ellisse e  l'ellisse, essendo a = b,  si riduce ad una  circonferenza  x² + y² = a²  di centro l'origine e raggio a

v si definisce eccentricità:

e misura quanto l’ellisse sia “schiacciata” e quanto più aumenta il valore di e tanto più l’ellisse è schiacciata; il valore limite di e = 1 è impossibile perché la misura della semidistanza focale si può avvicinare ma non può mai essere uguale a quella del semiasse maggiore, ovvero osservando che è  c < a  o c < b ,  a secondo se i fuochi si trovano rispettivamente sull’asse x sull’asse y,  il valore di e risulta compreso tra 0 e 1.

Osservazioni: Per determinare l’equazione canonica di un’ellisse, poiché in essa sono presenti due parametri incogniti, a e b, è sufficiente che siano note due condizioni, quali ad esempio:

Ø le lunghezze dei due semiassi

Ø le coordinate di un fuoco e un vertice (o semiasse)

Ø le coordinate di un fuoco (o di un vertice) e di un punto per il quale passa l’ellisse

Ø le coordinate di due punti per i quali passa l’ellisse

Ø le coordinate di un fuoco (o di un vertice) e l’eccentricità

………………………………………………………………………..

Esercizi svolti

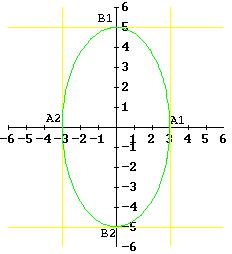
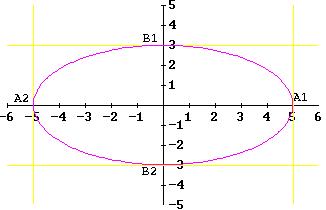
1) Un’ellisse ha per vertici i punti ( ± 5; 0) e per fuochi i punti ( ± 4; 0): 

a) scrivi l’equazione dell’ellisse

b) calcolane l’eccentricità

c) rappresentala graficamente

Ricordiamo, innanzitutto, che stiamo considerando un'ellisse in forma canonica, con i fuochi sull'asse x, come si evince dai dati del problema; in tal caso, l'equazione generale dell'ellisse assume la seguente forma:

con  a > b  (stessa equazione si avrebbe anche se i fuochi fossero sull'asse y, ma con a < b). 

Si possono determinare i valori dei coefficienti a e b, che ricordiamo rappresentano i semiassi e quindi quantità positive, utilizzando i dati forniti dal problema: ovvero, avendo noti A₁(5, 0) e A₂ (-5, 0)  e F₁(4, 0) e F₂ (-4, 0),  imponiamo le condizioni:

a = 5     e     c = 4

da cui:                                                

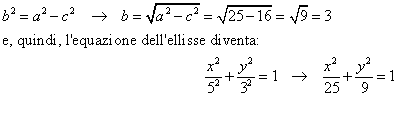
_{Gli altri due vertici avranno dunque coordinate B1(0, 3) e B2(0, -3); l'asse maggiore misura 10, l'asse minore 6.}

_{Pertanto possiamo calcolarci l'eccentricità come il rapporto tra la semidistanza focale e il semiasse maggiore, ossia:}

Per rappresentare graficamente l’ellisse basta tracciare i vertici e congiungerli con una linea curva inscritta al rettangolo di lati lunghi quanto gli assi dell’ellisse

2) Data l’ellisse di equazione :

a) calcolare le coordinate dei fuochi

b) il valore   dell’eccentricità

c) tracciare il grafico

Essendo a² = 9   e b² = 25, l’ellisse ha semiasse a = 3  e b = 5, i fuochi si trovano pertanto sull’asse maggiore y.

Determiniamo le coordinate dei fuochi dalla seguente relazione, tenendo in considerazione che è a <  b:

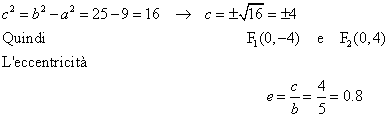
Per rappresentare graficamente l’ellisse, al solito tracciamo i vertici e li congiungiamo con una curva che deve risultare inscritta al rettangolo di lati lunghi quanto gli assi dell’ellisse: