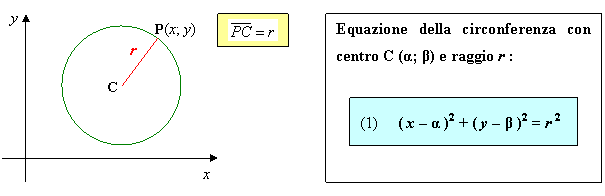
La circonferenza di  centro C (α; β) e raggio r è il luogo geometrico di tutti e soli i punti P(x; y) aventi da C distanza r :

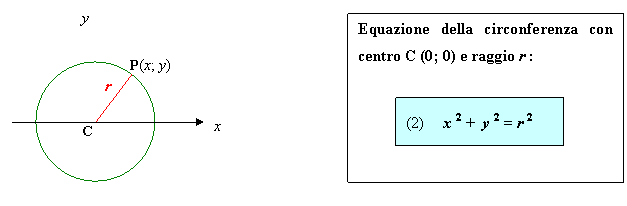
Sviluppando l’equazione (1) si ottiene l’equazione generale o canonica della circonferenza

che è un’equazione algebrica:

§ di 2° grado in x e in y

§ con i coefficienti di  x² e y² eguali tra loro

§ mancante del termine rettangolare in xy(che appare nell’equazione completa di 2° grado)

§ che rappresenta una circonferenza avente:

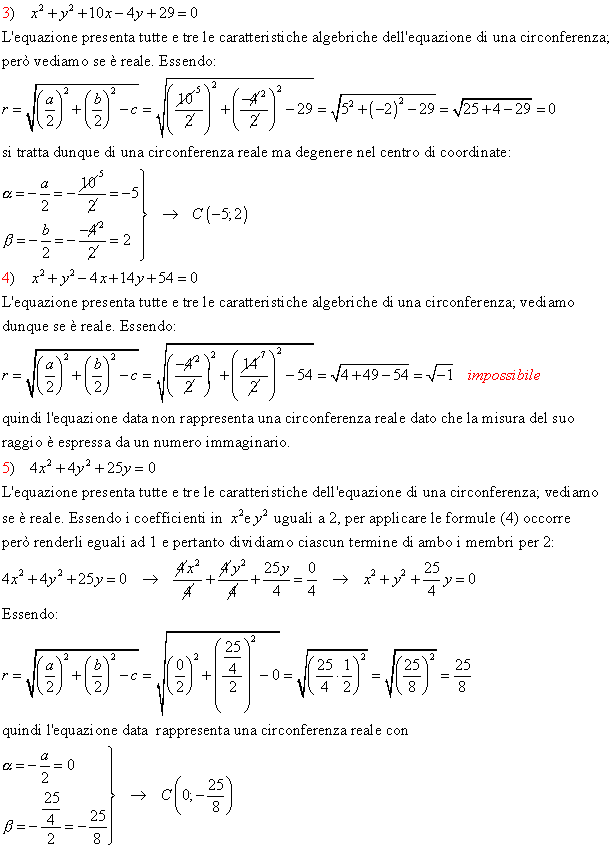
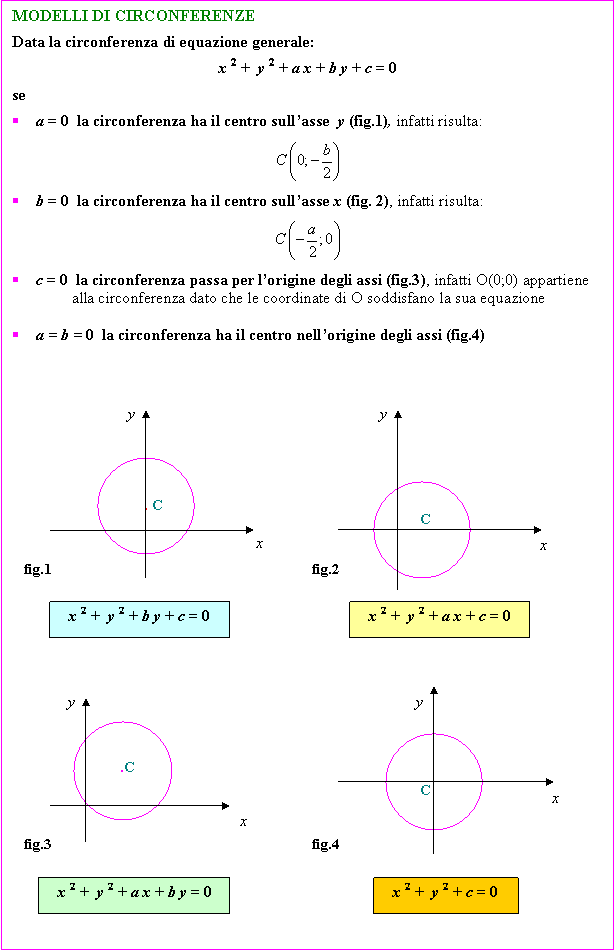
ESERCIZI GUIDATI

Individua il modello algebrico delle circonferenze rappresentate nei seguenti grafici:

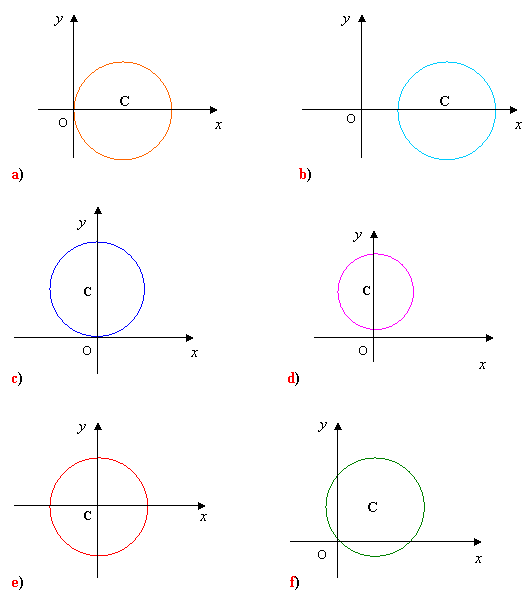
a)      La circonferenza:

§ passa per l’origine degli assi  →   c = 0

§ ha il centro C sull’asse x   →   b = 0

§ ha modello algebrico di tipo  x ² +  y ² + a x = 0

b)      La circonferenza:

§ ha il centro C sull’asse x  →  b = 0

§ ha modello algebrico di tipo:   x ² +  y ² + a x + c = 0

c)      La circonferenza:

§ passa per l’origine degli assi  →   c = 0

§ il centro C sta sull’asse y   →   a = 0

§ ha modello algebrico di tipo:   x ² +  y ² + b y = 0

d)      La circonferenza:

§ ha il centro C sull’asse y   →   a = 0

§ ha modello algebrico di tipo:   x ² +  y ² + b y + c = 0

e)      La circonferenza:

§ ha il centro C nell’origine degli assi →   a = b = 0

§ ha modello algebrico di tipo:   x ² +  y ² = r ²

f)      La circonferenza:

§ passa per l’origine degli assi  →   c = 0

§ ha modello algebrico di tipo:   x ² +  y ² + a x + b y = 0