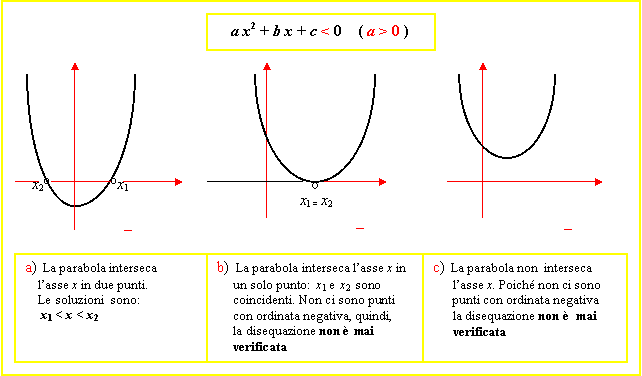
Data la disequazione (1) si possono presentare tre casi diversi, ovvero che la parabola intersechi l’asse x in due punti, in un punto o in nessun punto, in corrispondenza rispettivamente a :

a)  ∆ > 0,   b)  ∆ = 0,   c)  ∆ < 0. Stai attento, dobbiamo considerare i punti della parabola che sono situati nel semipiano positivo delle ordinate!

Esaminiamo, quindi i tre casi osservando le seguenti figure:

Analogamente, data la disequazione (2) si possono presentare tre casi diversi, ovvero che la parabola intersechi l’asse x in due punti, in un punto o in nessun punto, in corrispondenza rispettivamente a : a) ∆ > 0,  b) ∆ = 0,  c) ∆ < 0. Stai attento, dobbiamo considerare i punti della parabola che sono situati nel semipiano negativo delle ordinate!

Esaminiamo, quindi i tre casi osservando le seguenti figure:

N.B.: Si arrivano alle stesse conclusioni nel caso di disequazioni di 2° grado con il   coefficiente a < 0. Infatti, algebricamente basta moltiplicare ambo i membri della disequazione per “-1” e cambiare il simbolo di disequazione (se è “>” in “<” e viceversa). Geometricamente, invece le parabole presentano concavità rivolte verso il  basso però le soluzioni nei vari casi risulteranno le medesime di quelle individuate  precedentemente.

fig. 1

Se invece dobbiamo risolvere la disequazione:

x² + 4 x - 5 < 0

allora dobbiamo determinare i punti della parabola y = x² + 4 x - 5, la stessa dell’esercizio precedente, che si trovano però nel semipiano negativo delle ordinate, escluso l’asse x, vedi fig.2; quindi la disequazione è verificata per  -5 < x < 1 :

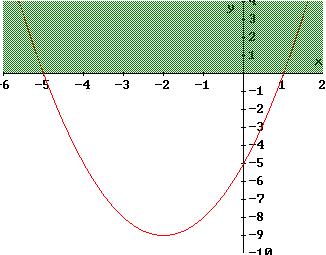
fig. 2

2.  Risolvere la seguente disequazione:

3 x² -6 x + 5 > 0

Graficamente significa che dobbiamo determinare i punti della parabola  y = 3 x² -6 x + 5 che si trovano nel semipiano positivo delle ordinate, escluso l’asse x . Determiniamo, dunque, i punti d’intersezione della parabola con l’asse delle x; a tal fine dobbiamo risolvere l’equazione:

3 x² -6 x + 5 = 0  →  ∆ < 0

Dunque la parabola non interseca l’asse x e, avendo la concavità rivolta verso l’alto, giace interamente nel semipiano positivo delle ordinate, vedi fig. 3. La disequazione è quindi verificata per qualsiasi valore di x.

fig. 3

Se invece dobbiamo risolvere la disequazione:

3 x² -6 x + 5 < 0

allora dobbiamo determinare i punti della parabola y = 3 x² -6 x + 5, la stessa dell’esercizio precedente, che si trovano però nel semipiano negativo delle ordinate, escluso l’asse x, vedi fig.4. La disequazione quindi non è  mai verificata, perché come si osserva giace interamente nel semipiano  y > 0.

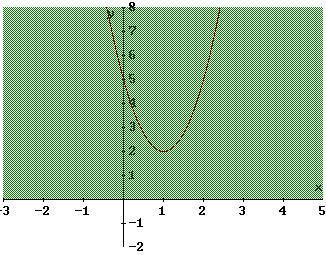
fig. 4

3. Risolvere la seguente disequazione:

x² -8 x + 16 >0

Dobbiamo determinare i punti della parabola  y = x² -8 x + 16 che si trovano nel semipiano positivo delle ordinate, escluso l’asse x. Determiniamo i punti d’intersezione tra la parabola e l’asse x, risolvendo l’equazione:

x² -8 x + 16 = 0   →   ∆ = 0    → x₁ =  x₂ = 4

L’equazione quindi ha due soluzioni coincidenti; ciò significa che la parabola, volgendo la concavità verso l’alto, è tangente all’asse x nel punto A(4; 0), come si vede in fig. 5. Pertanto, tutti i punti della parabola si trovano nel semipiano positivo delle ordinate, tranne il punto A che è il vertice e si trova nell’asse x. Perciò la disequazione è verificata per ogni x diverso da 4.

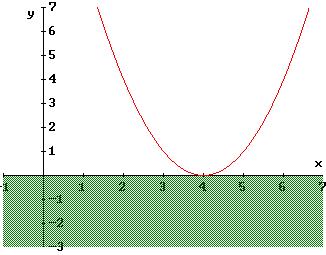
fig. 5

Se invece dobbiamo risolvere la disequazione:

x² -8 x + 16 < 0

allora dobbiamo determinare i punti della parabola y = x² -8 x + 16, la stessa dell’esercizio precedente, che si trovano però nel semipiano negativo delle ordinate, escluso l’asse x, vedi fig.6. La disequazione quindi non è  mai verificata, perché giace in y > 0.

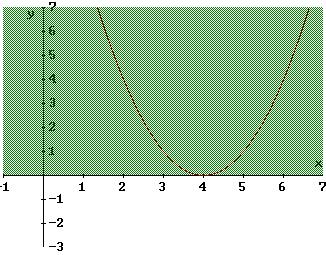
fig. 6