Una volta ridotta la disequazione di grado superiore al 2° o la disequazione frazionaria nella forma :

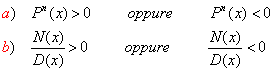
ovvero trasportati tutti i termini al primo membro della disequazione, in modo che al secondo membro compaia solo lo zero, risolvere la disequazione data significa stabilire quando il polinomio Pⁿ (x) o il rapporto tra N(x) e D(x) è positivo oppure negativo, a seconda del segno di disuguaglianza. Stai attento!  Il denominatore di una disequazione fratta non si elimina perché non conosciamo il suo segno.

Procediamo per la risoluzione di siffatte disequazioni in tal modo:

1. Scriviamo l’espressione a primo membro della a) come prodotto di polinomi di primo o di secondo grado in x, tramite scomposizione in fattori, oppure l’espressione a primo membro della b) come un’unica frazione avente per numeratore e per denominatore polinomi di primo o secondo grado in x oppure prodotti di tali polinomi, dato che siamo in grado di risolvere disequazioni di 1° o di 2° grado.

2. Studiamo il segno di ciascun polinomio scomposto di 1° o di 2° grado al variare della x. A tal scopo basterà risolvere la disequazione che si ottiene ponendo tale fattore maggiore di zero dato che nel restante intervallo- soluzione il relativo segno sarà negativo. Stai attento quando il segno di una disequazione frazionaria include anche il simbolo di “ = “; in tal caso il segno si considera solo per il numeratore perché il denominatore non si annulla mai, altrimenti la frazione e di conseguenza la disequazione perderebbe di significato.

3. Riportiamo in un quadro riassuntivo dei segni, ovvero in uno schema grafico che  riassume il variare dei segni dei polinomi fattori, delle rette o linee parallele che saranno continue in corrispondenza dei valori di x per cui il rispettivo fattore è positivo e tratteggiate in corrispondenza dei valori di x per cui è negativo. In prossimità degli eventuali zeri dei polinomi, se esclusi dal segno di disuguaglianza, perché strettamente “ > “ oppure “ < “,  metteremo un tondino; se inclusi metteremo invece un asterisco.

4. Per ogni singolo intervallo che si individua sulla retta dei numeri si applica la regola del prodotto dei segni per  determinare l’insieme delle soluzioni della disequazione.

Compiliamo il quadro dei segni e determiniamo il segno della disequazione data con la regola del prodotto dei segni:

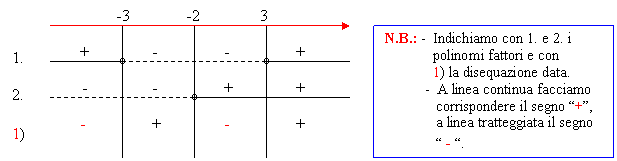
Pertanto la disequazione è verificata per:

x < -3  V  -2 < x < 3

Compiliamo il quadro dei segni:

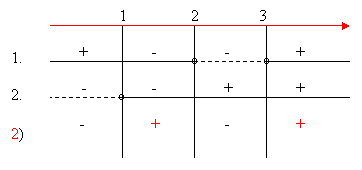
La disequazione è verificata per:        1 < x < 2  V x > 3

Compiliamo il quadro dei segni:

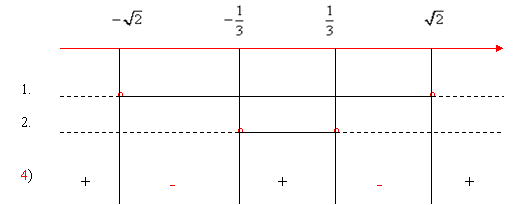La disequazione è verificata per:

Compiliamo il quadro dei segni:

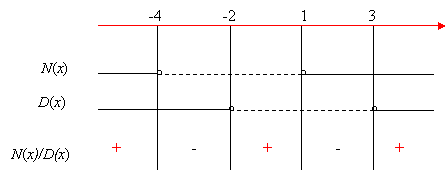
Disequazione verificata per

 x < - 4 V – 2 < x <1 V x >3.

Compiliamo il quadro dei segni:

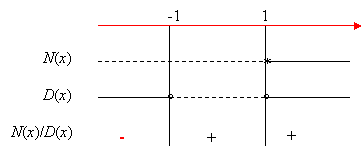
La disequazione è verificata per       x ≤ -1 .

Compiliamo il quadro dei segni:

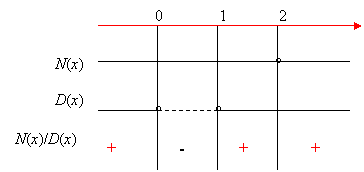
La disequazione è verificata per  x < 0 V 1 < x < 2 V x > 2 .

Compiliamo il quadro dei segni:

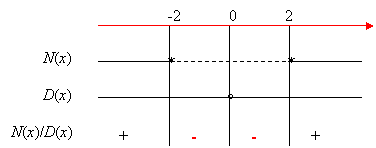
La disequazione è verificata per     -2 < x < 0 V 0 < x < 2.

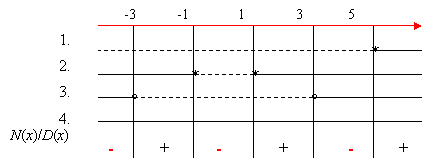
La disequazione è verificata per  x < -3 V  -1 ≤  x ≤ 1  V  3 < x ≤ 5 .