Un sistema di disequazioni è un insieme di disequazioni nella stessa incognita e quindi per risolvere tale sistema dobbiamo cercare le soluzioni comuni, ovvero trovare quei numeri reali che soddisfano contemporaneamente tutte le disequazioni.

Una volta ridotto il sistema in forma normale, procediamo per la risoluzione nel seguente modo:

1. Risolviamo singolarmente ciascuna disequazione del sistema

2. Rappresentiamo graficamente nel quadro dei segni, l’insieme delle soluzioni di ciascuna disequazione

3. Esaminando tale quadro grafico individuiamo facilmente gli intervalli che soddisfano tutte le disequazioni costituenti il sistema perché sono rappresentati da linee tutte continue; l’insieme di tali intervalli costituisce quindi la soluzione del sistema. Nel caso in cui gli intervalli non soddisfano contemporaneamente tutte le disequazioni, per cui sono rappresentati graficamente da linee non tutte continue, allora l’insieme delle soluzioni del sistema è vuoto. Può anche verificarsi che un intervallo di soluzioni si riduca a un solo numero reale.

ESERCIZI GUIDATI

Risolviamo i seguenti sistemi di disequazioni:

Riportiamo graficamente le soluzioni delle singole disequazioni nel quadro dei segni:

Esaminando il quadro grafico si individuano linee tutte continue solo nell’intervallo colorato in giallo, pertanto soluzione del sistema è l’intervallo: 2 < x < 3.

Compiliamo il quadro dei segni:

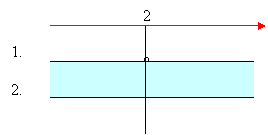
Come si osserva, 2 verifica la disequazione 2. ma non la 1. quindi non è soluzione comune.

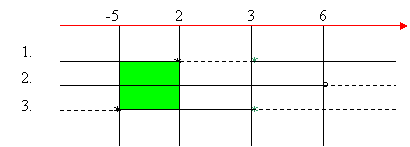
Come si osserva oltre l’intervallo, colorato in verde,  le tre disequazione hanno in comune anche l’intervallo ridotto al solo elemento 3, quindi soluzioni del sistema sono:   -5 ≤ x ≤ 2  V  x = 3.

Compiliamo il quadro per determinare con la regola dei segni gli intervalli di negatività della disequazione fratta:

Disequazione verificata per  0 < x < 1. Tale intervallo rappresenta, per quanto detto precedentemente, la soluzione del sistema.