v Sistemi di Disequazioni in due variabili
Per risolvere un sistema di disequazioni:
1. si risolvono le singole disequazioni del sistema, rappresentando le relative soluzioni nel medesimo piano cartesiano Oxy
2. si determina l’insieme d’intersezione delle parti di piano che rappresentano le soluzioni delle disequazioni
Esercizio guidato
Risolvere il seguente sistema di disequazioni:

Rappresentiamo nel piano cartesiano le soluzioni della disequazione:
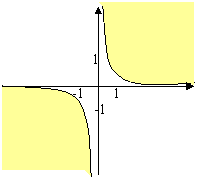
y – x2>0, y > x2 parabola con asse di simmetria l’asse y e vertice in O che andiamo a rappresentare nel medesimo piano Oxy:
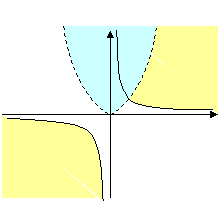
Le parti comuni agli insiemi delle soluzioni delle due disequazioni costituiscono le soluzioni del sistema, ossia graficamente:
 |
v Disequazioni fratte
Per risolvere la seguente disequazione:
![]()
basta ricordare che una frazione è positiva quando numeratore e denominatore sono concordi, pertanto bisogna porre numeratore e denominatore entrambi positivi o entrambi negativi e quindi risolvere i due sistemi di disequazioni così ottenuti: l’unione delle soluzioni dei sistemi saranno le soluzioni della disequazione fratta:

![]()
ricordando che una frazione è negativa quando numeratore e denominatore sono disconcordi, bisogna porre numeratore positivo e denominatore negativo o, viceversa, numeratore negativo e denominatore positivo e quindi risolvere i due sistemi di disequazioni così ottenuti: l’unione delle soluzioni dei sistemi saranno le soluzioni della disequazione fratta:
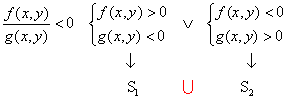
Esercizio guidato
Risolvere la seguente disequazione fratta:

Rappresentiamo nel piano Oxy le soluzioni del sistema, dato dall’insieme intersezione dei punti del piano che rappresentano le soluzioni delle singole disequazioni, colorate in giallo più intenso:
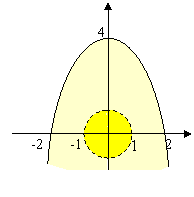
Risolviamo ora il secondo sistema :
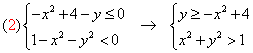
Rappresentiamo nel piano Oxy le soluzioni del sistema (2), dato dall’insieme intersezione dei punti del piano che rappresentano le soluzioni delle singole disequazioni, colarate in giallo più intenso:
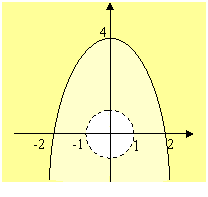
Le soluzioni della disequazione fratta sono date, dunque, dall’unione delle soluzioni dei due sistemi (in giallo intenso), qui di seguito rappresentate:

v Disequazioni in valore assoluto
Tieni presente, in analogia alle disequazioni in una sola variabile in modulo, che:
Ø
![]() intersezioni delle soluzioni
intersezioni delle soluzioni
Ø
![]() unione delle soluzioni
unione delle soluzioni
Esercizi guidati
Risolvere le seguenti disequazioni in modulo:
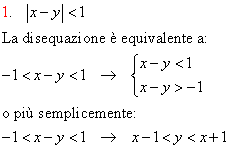
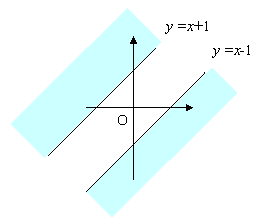
quindi, le soluzioni dell’equazione sono date o dall’insieme intersezione dei punti del piano che soddisfano il sistema o in modo equivalente, ma più semplicemente, dalla regione di piano (colorata) delimitata dalle due rette y =x+1 e y =x-1 , illimitata e aperta, perché non contiene i punti delle rette che la delimitano, graficamente la regione colorata:


pertanto soluzioni della disequazione data sono i semipiani (colorati) esterni alle due rette, illimitati e chiusi, in quanto comprendono tutti i punti della retta origine (frontiera), vedi la rappresentazione grafica: