Disequazioni irrazionali (di funzioni polinomiali)

· Una disequazione si dice irrazionale quando in essa compaiono uno o più  radicali contenenti l’incognita x. Per es.:

· Ricordiamo che il radicale aritmetico, come ad es. la 1) e 2), cioè la radice di indice pari esiste solo se il suo radicando è un numero non negativo, cioè un numero positivo o nullo, non dimentichiamo quindi di prendere in considerazione questa condizione di realtà ogni volta che siamo in presenza di radice di indice pari .

· Ricordiamo invece che esiste la radice di indice dispari anche dei numeri negativi,        

· Quindi  nel caso che il radicando sia un polinomio, vedi es. 3), esiste per ogni , cioè la radice cubica si  può sempre estrarre e pertanto non c’è alcuna condizione da prendere in esame. Pertanto per risolvere una disequazione irrazionale contenente radici cubiche basta risolvere la       disequazione razionale che si ottiene elevando ambo i membri della disequazione di partenza al       cubo, perché si ottiene una disequazione equivalente, cioè che ammette le stesse soluzioni di quella       data. Si ha quindi, per n dispari:

1)  Risoluzioni di disequazioni del tipo:

Compiliamo il quadro dei segni e prendiamo le soluzioni comuni ossia gli intervalli che verificano contemporaneamente le tre disequazioni:

Le soluzioni della disequazione data sono dunque:

1) Risoluzioni di disequazioni del tipo:

Anche in questo caso occorre porre la condizione di esistenza del radicale

A differenza del caso precedente nel quale il verso della disequazioni era l’opposto di quello qui considerato, il secondo membro della 1), cioè B(x), può essere sia positivo sia negativo o nullo, in quanto se A(x) è positivo può essere maggiore di un numero sia positivo sia negativo che nullo.

Nel caso in cui il secondo membro della 1) sia positivo o nullo, si potranno elevare ambi i membri della disequazioni alla potenza n-sima. Nel caso invece in cui B(x) sia negativo, la disequazioni stessa sarà soddisfatta purché sussista la 2): in tal caso infatti A(x) , essendo positivo o nullo, sarà senz’altro maggiore di una quantità negativa.

Pertanto l’insieme delle soluzioni della 1) sarà  dato dall’unione degli insiemi delle soluzioni dei seguenti sistemi:

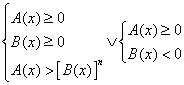
Poniamo adesso l’attenzione sul primo dei due sistemi. La condizione

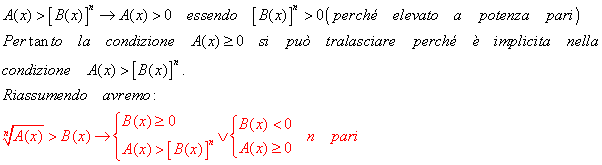
Pertanto, le soluzioni della disequazioni 1) sono date dall’unione delle soluzioni dei due sistemi.

Nel caso in cui la disequazioni 1) presenti il simbolo ≥, avremo:

Risolviamo adesso gli esercizi seguenti stando ben attenti alle procedure risolutive:

Esercizi guidati

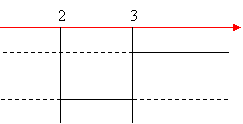Il sistema non avendo intervalli comuni non ha soluzione e pertanto le soluzioni della disequazioni di partenza saranno date, se esistono, solo da quelle del secondo sistema che andiamo a risolvere:

Quindi la disequazioni è verificata per : x < 3