Una disequazione si dice  esponenziale quando l’incognita compare nell’esponente di qualche potenza.

1. Disequazioni esponenziali i cui membri sono esprimibili in potenze aventi la stessa base, ovvero che  si possono ridurre nella forma canonica:

( 1 )       a ^{f ( x)}  > a ^{g ( x)} ,  con  a > 0 e a ≠ 0

     dove al posto del simbolo “ > “ può esserci, eventualmente, “ < “, “ ≤ “ oppure “ ≥ “.

Per risolvere tale disequazione esponenziale basta osservare la base e ricordare che:

§ la funzione esponenziale con base a > 1 è sempre crescente, cioè al crescere delle ascisse (gli esponenti) crescono le corrispondenti ordinate (le potenze) e viceversa; infatti osservando la curva esponenziale:

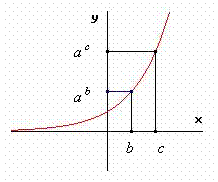
a ^c  > a ^b → c > b

     per cui la disequazione esponenziale è equivalente a una disequazione dello stesso verso tra gli esponenti di tali potenze, quindi in generale se:

a > 1,      a ^{f (x)} > a ^{g ( x)}   → f (x) > g (x)

§ la funzione esponenziale con base 0 < a < 1 è sempre decrescente, cioè al decrescere delle ascisse (gli esponenti) crescono le corrispondenti ordinate (le potenze) e viceversa; infatti osservando la curva esponenziale:

a ^c  > a ^b  →   c < b

per cui la disequazione esponenziale è equivalente a una disequazione di verso contrario tra gli esponenti di tali potenze, quindi in generale:

0 < a < 1,      a ^{f (x})  > a ^g(x)   → f (x) < g (x)

Esercizi Guidati

1. Modello: a ^{f (x})  > a ^g(x)  

2. Disequazione esponenziale risolvibile utilizzando un’ incognita ausiliaria:

3. Disequazioni esponenziali risolvibili con i logaritmi

Data la disequazione esponenziale ridotta nella seguente forma canonica:

a ^{f  (x)} > b ^{g ( x)}

ovvero i cui membri non sono riconducibili a potenze aventi la stessa base, per risolverla si prendono i logaritmi decimali (o neperiani) di ambo i membri (cosa lecita in quanto gli argomenti, potenze di numeri positivi, sono positivi) ed essendo la base del logaritmo “10” (o “e”) un numero maggiore di uno, sappiamo (vedi modello grafico della funzione logaritmica con  base a >1) che la funzione logaritmica è sempre crescente, ossia al crescere delle ascisse (gli argomenti) crescono le corrispondenti ordinate (i logaritmi), per cui la disequazione esponenziale è equivalente a una disequazione logaritmica dello stesso verso di ambo i membri, ovvero:

a ^{f  (x)} > b ^{g ( x)}    →  log a ^{f  (x)}  > log b ^{g ( x)}  

Applicando poi le proprietà dei logaritmi si determina la soluzione dell’equazione esponenziale.

Esercizi Guidati