Una disequazione si dice  logaritmica quando l’incognita compare nell’argomento di qualche

logaritmo.

1. TIPO

Disequazioni logaritmiche i cui membri sono esprimibili in un logaritmo della stessa base, ovvero che  si possono ricondurre nella forma canonica:

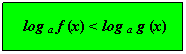
     dove al posto del simbolo “ > “ può esserci, eventualmente, “ < “, “ ≤ “ oppure “ ≥ “.

Prima di esplicitare i vari passi risolutivi di disequazioni di tal tipo, osserviamo la base e ricordiamo che:

§ la funzione logaritmica con base a > 1 è sempre crescente, cioè al crescere delle ascisse (gli argomenti) crescono le corrispondenti ordinate (i logaritmi) e viceversa; infatti osservando la curva logaritmica:

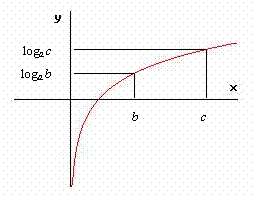
log_a c  > log_a b → c > b

     per cui la disequazione logaritmica è equivalente a una disequazione dello stesso verso tra gli argomenti dei logaritmi; quindi in generale se:

a > 1,      log_a f (x)  > log_a g (x)   → f (x) > g (x)

§ la funzione logaritmica con base 0 < a < 1 è sempre decrescente, cioè al decrescere delle ascisse (gli argomenti) crescono le corrispondenti ordinate (i logaritmi) e viceversa; infatti osservando la curva logaritmica:

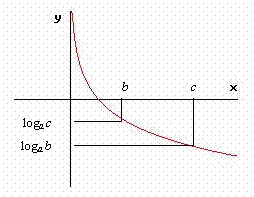
log_a c  > log_a b → c < b

pertanto la disequazione logaritmica è equivalente a una disequazione di verso contrario tra gli argomenti dei logaritmi; quindi in generale se:

a > 1,      log_a f (x)  > log_a g (x)   → f (x) > g (x)

Per risolvere, dunque,  le disequazioni logaritmiche riconducibili al 1° Tipo, procediamo nel seguente modo:

§ determiniamo il dominio o C.E. della disequazione (imponendo le condizioni di esistenza dei logaritmi)

§ trasformiamo, eventualmente,  la disequazione nella forma canonica,  ovvero esprimiamo ciascun membro della disequazione in un  logaritmo della stessa base, applicando le proprietà dei logaritmi;

§ si passa dalla disequazione logaritmica alla disequazione degli argomenti che per risolverla si deve tener presente la base del logaritmo, ovvero:

§ per a > 1         se      log_a f (x)  > log_a g (x)   → f (x) > g (x)

§ per 0 < a < 1   se      log_a f (x)  > log_a g (x)   → f (x) > g (x)

§ risolviamo, infine, il sistema formato dal dominio o C.E. della disequazione  e dalle soluzione della disequazione tra gli argomenti, per l’accettabilità delle soluzioni determinate.

Esercizi Guidati

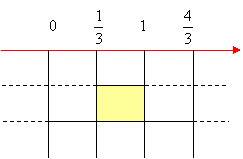
Compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

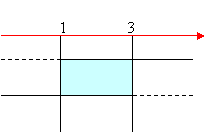
La disequazione ha per soluzioni: 1 < x < 3.

Compiliamo il quadro dei segni:

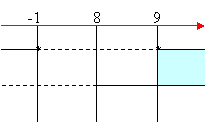
Soluzione della disequazione: x ≥ 9.

Compiliamo il quadro dei segni:

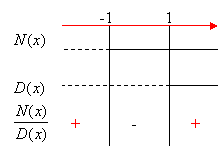
la disequazione è verificata per  x < -1  V x > 1.

2. TIPO

Disequazioni logaritmiche risolvibili utilizzando un’ incognita ausiliaria

Esercizi Guidati

E’ evidente la soluzione, in ogni caso compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

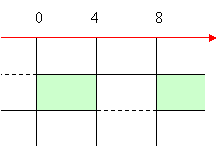
quindi soluzione della disequazione data è  0 < x < 4  V x > 8.