Scriviamo la disequazione in forma canonica:

cos  x > b     o   cos x <  b      con   -1 ≤  b ≤  1

dove al posto di “ < “ o “ > “ può esserci  il simbolo  di “ ≤ ” o “≥” .

Si tratta di determinare per quali valori dell’angolo x il coseno assume valori maggiori oppure  minori di b.

Poiché il coseno di un angolo rappresenta l’ascissa del punto della circonferenza goniometrica, risolvere le disequazioni date significa determinare gli angoli corrispondenti ai punti della circonferenza goniometrica aventi ascissa maggiore oppure minore di b.

Il problema pertanto si risolve ancora trovando questi punti e, quindi,  gli angoli al centro ad essi associati.

In generale:

1. consideriamo l’equazione ad essa associata:      

      Si tratta di determinare i punti della circonferenza goniometrica aventi ascissa b e di      conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati.

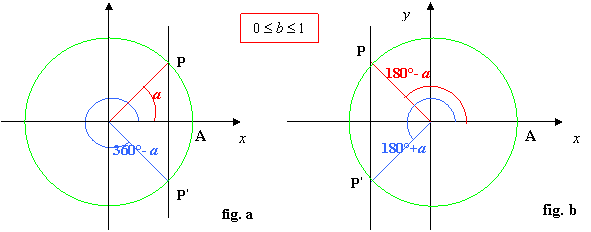
2. Determiniamo tali punti : disegniamo la circonferenza goniometrica e la retta parallela all’asse delle y,   x = b; tale retta, se -1≤ b ≤1,  intersecherà la circonferenza in due punti P e P’, aventi stessa ascissa b, vedi figure:

3. Determiniamo gli angoli associati ai punti: congiungiamo i punti P e P’ al centro della circonferenza e consideriamo i due angoli associati aventi come lato origine OA e aventi come secondo lato rispettivamente OP e OP’; indichiamo con a il minimo angolo tale che  cos x = I b I, vedi figure:

y

4. Per determinare le soluzioni si osserva il verso della disequazione data :

§ se è strettamente “ > “ o “ < “ i punti associati agli angoli vengono esclusi; in caso di “ ≤ ” o “≥” tali punti saranno inclusi tra le soluzioni della disequazione

§ se è cos x > b allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta a destra della retta  x = b; precisamente, partendo dall’origine A degli archi si ha:

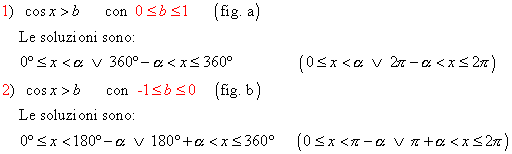
§ se è cos x < b   allora le soluzioni sono date dai punti della parte di circonferenza o dell’arco, che sta a sinistra della retta  x = b; precisamente:

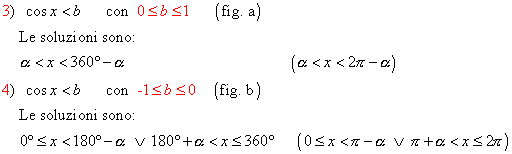
5. Per determinare le infinite soluzioni in R: aggiungiamo alle soluzioni trovate in [0;360°]  i multipli di 360° ( 2 π ), per la periodicità della funzione seno.

ESERCIZI GUIDATI

Risolvere le seguenti disequazioni goniometriche elementari in coseno:

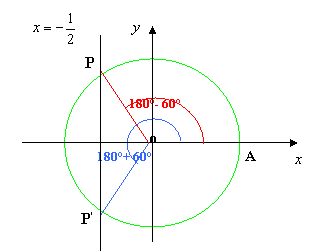
Le soluzioni dell’equazione associata sono dunque:        x = 120°    e  x = 240°

Mentre le soluzioni della disequazione sono dati dagli angoli associati ai punti dell’arco di circonferenza situato a sinistra della retta , esclusi i punti, ovvero:

120° < x < 240°