Scriviamo la disequazione in forma canonica:

tg  x > b     o   tg x <  b      con   - ∞ < b < + ∞

dove al posto di “ < “ o “ > “ può esserci  il simbolo  di “ ≤ ” o “≥” .

Si tratta di determinare per quali valori dell’angolo x la tangente assume valori maggiori oppure  minori di b.

In generale:

1. consideriamo l’equazione ad essa associata:       

      Si tratta di determinare i punti della circonferenza goniometrica aventi stessa tangente e di      conseguenza le soluzioni sono le ampiezze degli angoli ad essi associati.

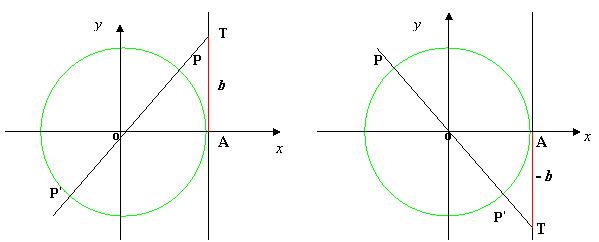
2. Determiniamo tali punti : disegniamo la circonferenza goniometrica e la retta tangente alla circonferenza nel punto A, origine degli archi. Su  tale retta individuiamo il punto T la cui ordinata è b. Tracciamo la retta del diametro passante per T; questa incontra la  circonferenza nei due punti P e P’ aventi la tangente uguale a b, vedi figure:

3. Determiniamo gli angoli associati ai punti: partendo, al solito, dall’ origine A degli archi  si individuano i due angoli AÔP e AÔP’ angoli associati ai punti P e P’aventi stessa tangente; con a il minimo angolo tale che tg x = I b I, cioè a è l’ampiezza dell’angolo positivo,vedi figure:

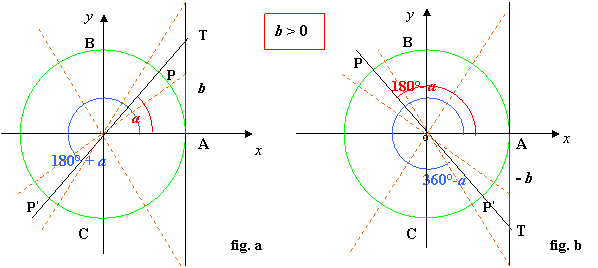
4. Per determinare le soluzioni si osserva il verso della disequazione data :

§ se è strettamente “ > “ o “ < “ i punti associati agli angoli vengono esclusi; in caso di “ ≤ ” o “≥” tali punti saranno inclusi tra le soluzioni della disequazione

§ se è  tg x > b ,  come in fig. a, osservando le rette del diametro tratteggiate e passanti per T, si intuisce che le soluzioni sono date dagli angoli associati ai punti che stanno o nell’arco PB o nell’arco P’C, esclusi oltre i punti B e C, perché a 90° e a 270° non è definita la tangente , anche i punti P e P’ perché la disuguaglianza è stretta; mentre osservando la  fig. b le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi  AB , PC e P’A, esclusi oltre i punti B e C anche i punti P e P’; precisamente:

§ se è  tg x < b ,  come in fig. a, osservando le rette del diametro tratteggiate e passanti per T, si intuisce che le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi  AP, BP’ e CA, esclusi oltre i punti B e C, ove non esiste la tangente, anche i punti P e P’ perché la disuguaglianza è stretta; mentre osservando la  fig. b le soluzioni sono date dagli angoli associati ai punti che stanno sugli archi  BP e CP’, esclusi i punti; precisamente:

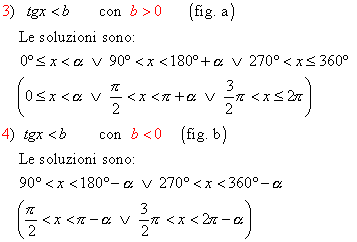
5. Per determinare le infinite soluzioni in R: si aggiungono alle soluzioni che cadono solo  in [0°;180°] i  multipli di 180° ( π ), per la periodicità della funzione tangente: x = a + k180° oppure  x = a + kπ .

ESERCIZI GUIDATI

Risolvere le seguenti disequazioni goniometriche elementari in tangente:

1)    tgx < 1           con  0° ≤ x ≤ 360°

Con l’aiuto della circonferenza goniometrica e la definizione di tangente di un angolo, ricerchiamo gli angoli x la cui tangente è 1.

Disegniamo, dunque, la circonferenza goniometrica e la retta ad essa tangente nel punto A; riportiamo sulla retta il punto T di ordinata 1. Tracciamo la retta del diametro passante per T che intersecherà la circonferenza nei due punti P e P’ ai quali corrispondono gli angoli a e 180° + a, con a = 45° essendo tg 45° =1, vedi figura :

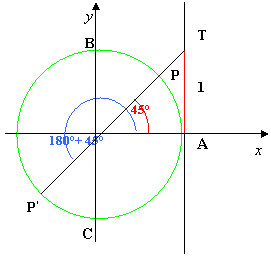
Quindi le soluzioni dell’equazione tg x = 1 associata alla disequazione sono: x = 45°   e  x = 225°

Si vede chiaramente che gli angoli la cui tangente è maggiore di 1 sono associati a quei punti che cadono o nell’arco AP, o nell’arco BP’ o nell’arco CA, esclusi oltre  i punti B e C, ove non esiste la tangente, anche i punti P e P’ perché la disuguaglianza è stretta. Pertanto le soluzioni della disequazione nell’intervallo [0°; 360°] sono:

0° ≤ x < 45°   V  90° < x < 225°   V   270° < x ≤ 360°

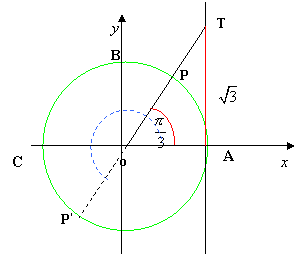
Poiché per la disequazione  sono richieste le soluzioni in R, consideriamo per la periodicità della funzione tangente il solo angolo che cade in [0; π ], cioè nella semicirconferenza situata nel 1° e 2° quadrante; pertanto i punti di ordinata minore di  sono quelli che cadono o nell’arco AP o nell’arco BC, con esclusione del solo punto B, dato che a  la tangente non è definita.

La disequazione, dunque, nell’intervallo [0; π ], è verificata per

pertanto in R le soluzioni si ottengono aggiungendo alle soluzioni precedenti i multipli di π, ovvero:

3)  

Scriviamo la disequazione in forma canonica:

Si tratta di determinare gli angoli x la cui tangente è maggiore di . Per determinare tali soluzioni ci serviamo, come al solito, della circonferenza goniometrica. Tracciata dunque la circonferenza goniometrica e la retta tangente nel punto A, individuiamo su tale retta il punto T di ordinata  e i punti P e P’ della circonferenza ad esso associati, vedi figura:

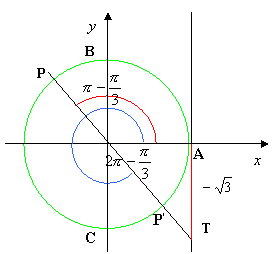
Le soluzioni dell’equazione associata alla disequazione sono:

Come si osserva dalla figura, vedi anche schema generale delle soluzioni, tutti e soli gli angoli aventi tangente maggiore di  sono quelli associati ai punti della circonferenza che si trovano o nell’arco AB o nell’arco PC o nell’arco P’A, esclusi oltre i punti B e C, in cui non è definita la tangente, anche i punti P e P’, essendo stretta la disuguaglianza; pertanto le soluzioni della disequazione sono: