Dovendo risolvere adesso le disequazioni goniometriche non elementari ma ad esse riconducibili, è bene rivedere:
§ Le Premesse alle disequazioni goniometriche
§ Lo Schema riassuntivo delle disequazioni elementari
§ Lo Schema riassuntivo delle disequazioni algebriche di 2° grado
In generale:
si procede cercando, dapprima, di rendere uguali gli argomenti, se diversi, delle funzioni presenti e, poi, di trasformare, mediante l’utilizzo di relazioni o formule goniometriche, la disequazione in una sola funzione goniometrica, sempre nel caso in cui siano presenti più funzioni, e quindi in una o più disequazioni elementari.
ESERCIZI GUIDATI
Risolvere le seguenti disequazioni goniometriche:


Come si
osserva la condizione composta: ![]() è verificata per tutti gli
archi di circonferenza situati
all’interno delle due rette parallele all’asse delle x, ovvero gli archi PB e BP’ escluso i punti trattandosi di una disuguaglianza stretta;
pertanto, partendo dall’origine A degli archi, le soluzioni nell’intervallo
[0; 2π] sono:
è verificata per tutti gli
archi di circonferenza situati
all’interno delle due rette parallele all’asse delle x, ovvero gli archi PB e BP’ escluso i punti trattandosi di una disuguaglianza stretta;
pertanto, partendo dall’origine A degli archi, le soluzioni nell’intervallo
[0; 2π] sono:
![]()


Come si osserva
la condizione composta:![]() è verificata per tutti archi di circonferenza situati all’esterno delle due rette parallele
all’asse delle x, ovvero o l’arco PP’ o l’arco P’’P’’’, escluso i punti trattandosi ancora di una disuguaglianza
stretta; pertanto, partendo dall’origine A degli archi, le soluzioni
nell’intervallo [0; 2π] sono:
è verificata per tutti archi di circonferenza situati all’esterno delle due rette parallele
all’asse delle x, ovvero o l’arco PP’ o l’arco P’’P’’’, escluso i punti trattandosi ancora di una disuguaglianza
stretta; pertanto, partendo dall’origine A degli archi, le soluzioni
nell’intervallo [0; 2π] sono:
![]()


Come si osserva
la condizione composta: ![]() è verificata per tutti
gli archi di circonferenza situati all’interno delle due rette parallele
all’asse delle y, ovvero gli archi PP’ e P’’P‘’’ escluso i punti trattandosi di una disuguaglianza stretta;
pertanto, partendo dall’origine A degli archi, le soluzioni nell’intervallo
[0; 2π] sono:
è verificata per tutti
gli archi di circonferenza situati all’interno delle due rette parallele
all’asse delle y, ovvero gli archi PP’ e P’’P‘’’ escluso i punti trattandosi di una disuguaglianza stretta;
pertanto, partendo dall’origine A degli archi, le soluzioni nell’intervallo
[0; 2π] sono:


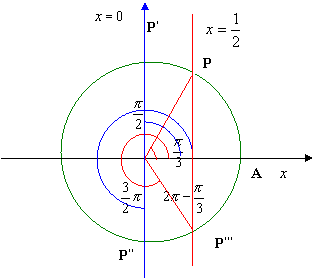
Come si
osserva la condizione composta:![]() è verificata per tutti gli archi di circonferenza
situati all’esterno delle due rette parallele all’asse y ovvero o per l’arco P’’’P o per l’arco P’P’’, escluso i punti stessi trattandosi ancora di una
disuguaglianza stretta; pertanto, partendo dall’origine A degli archi, le
soluzioni nell’intervallo [0; 2π] sono:
è verificata per tutti gli archi di circonferenza
situati all’esterno delle due rette parallele all’asse y ovvero o per l’arco P’’’P o per l’arco P’P’’, escluso i punti stessi trattandosi ancora di una
disuguaglianza stretta; pertanto, partendo dall’origine A degli archi, le
soluzioni nell’intervallo [0; 2π] sono:



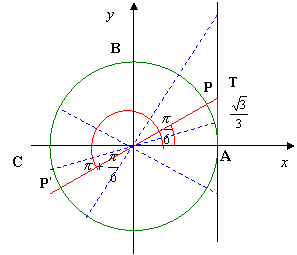
Si tratta di determinare, con l’aiuto della circonferenza goniometrica, gli angoli X aventi tangente o minore di -1 o maggiore di 0.
Tracciamo la circonferenza goniometrica e la tangente in A, dove riportiamo i valori -1 e 0 che coincide con A:
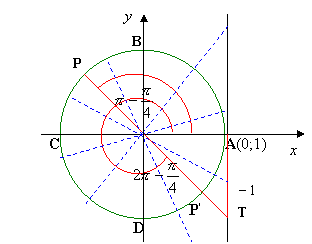
Come si osserva gli angoli aventi tangente positiva o minore di -1 sono associati ai punti che stanno o sull’arco AB o sull’arco BP o sull’arco CD o sull’arco DP’, escluso gli estremi degli archi ; pertanto, partendo dall’origine degli archi A, le soluzioni in [0; 2π] sono:




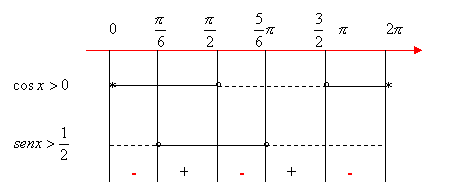
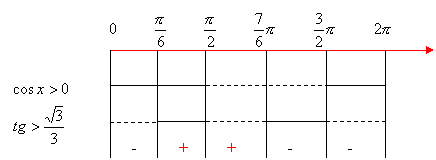
Compiliamo il quadro riassuntivo dei segni:


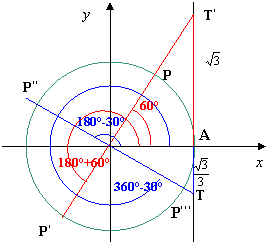
![]() Come si osserva, verificano
la condizione composta gli archi P’’’P
e P’’P’, escluso i punti estremi essendo una
disuguaglianza stretta; partendo dall’origine A degli archi, si hanno dunque
le soluzioni:
Come si osserva, verificano
la condizione composta gli archi P’’’P
e P’’P’, escluso i punti estremi essendo una
disuguaglianza stretta; partendo dall’origine A degli archi, si hanno dunque
le soluzioni:
0°< x <60° V 150°< x < 240° V 330°< x < 360°

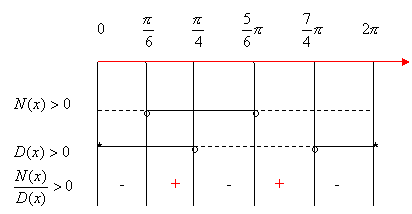
Come si osserva, le soluzioni della disequazione data sono:

Compiliamo il quadro dei segni:
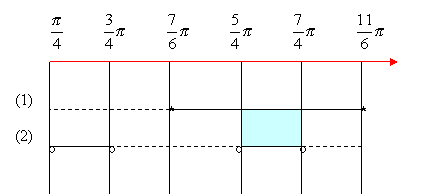
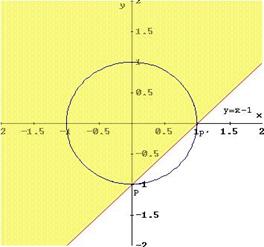
La parte
colorata in celeste individua gli intervalli comuni alle due disequazioni,
quindi il sistema dato è verificato per ![]() , escluso gli estremi perché soluzioni
della (1) e non della (2).
, escluso gli estremi perché soluzioni
della (1) e non della (2).