Prima di trattare le disequazioni goniometriche, è bene RICORDARE che:
§ considerato un angolo orientato a in una circonferenza goniometrica, che in fig. 1 abbiamo supposto nel primo quadrante, ad esso resta associato il punto P della circonferenza che ha per ascissa il coseno di a ed ordinata il seno di a:

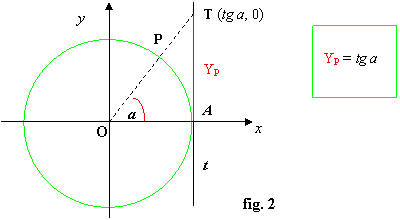
§ la tangente di a in una circonferenza goniometrica, vedi fig. 3, è l’ordinata del punto T d’intersezione tra la retta t tangente alla circonferenza nel punto A, origine degli archi, con il prolungamento del secondo lato OP dell’angolo a:
§ tracciando dal punto P, secondo estremo dell’arco a, la parallela all’asse x, vedi fig. 3, questa incontra la circonferenza nel punto P’ associato all’angolo al centro 180° - a; conducendo poi i diametri PP’’ e P’P’’’ restano individuati i punti P’’, associato all’angolo al centro 180° + a, e P’’’, associato all’angolo al centro 360° - a o all’equivalente angolo opposto – a:
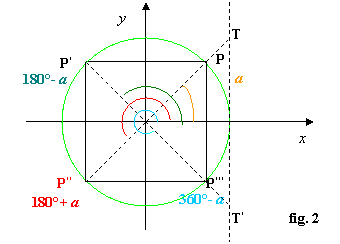
questi angoli così determinati vengono chiamati angoli associati; in particolare:
1. gli angoli associati, cioè che corrispondono, ai punti P e P’( a e 180°-a) ed ai punti P’’e P’’’(180°+ a e 360°- a), disposti su corde parallele all’asse delle x, hanno stessa ordinata, cioè medesimo seno di a
2. gli angoli associati ai punti P e P’’’(a e 360°- a) ed ai punti P’ e P’’(180°-a e 180°+ a), disposti su corde parallele all’asse delle y, hanno stessa ascissa, cioè medesimo coseno di a
3. gli angoli associati ai punti P e P’’(a e 180° + a) ed ai punti P’e P’’’(180°- a e 360°- a), disposti diagonalmente, hanno medesima tangente di a
§ proprietà fondamentali delle funzioni goniometriche di base e delle rispettive inverse:
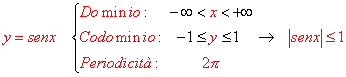
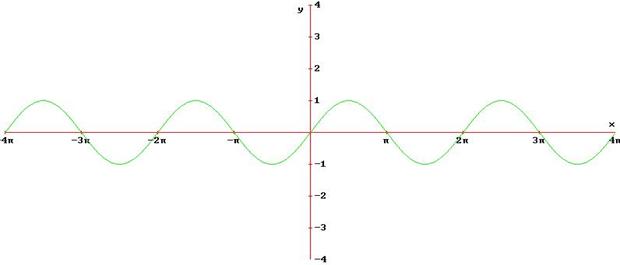
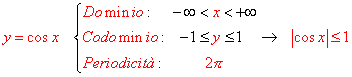
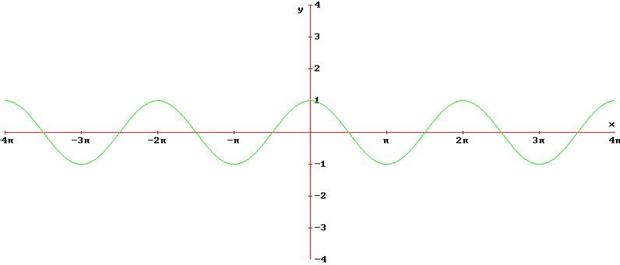

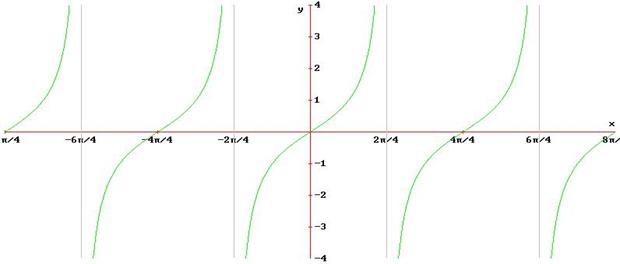
Funzioni inverse
I grafici delle funzioni inverse si ottengono per simmetria dei grafici delle rispettive funzioni dirette, negli intervalli ove però tali funzioni risultano o solo crescenti o solo decrescenti, rispetto alla bisettrice del 1° e 2° quadrante.


![]()

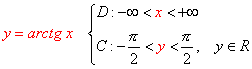

§ angoli, relazioni e formule goniometriche di base per la risoluzione di semplici ma fondamentali disequazioni goniometriche:
