Ricordiamo le seguenti Definizioni e Proprietà dei logaritmi:

Risoluzione di equazioni logaritmiche
Un’equazione si dice logaritmica quando l’incognita figura nell’argomento di qualche logaritmo.
Come ad esempio log 3 x - 9 = 0; non lo è log 2 8 = 5x in quanto la x non figura nell’argomento del logaritmo.
Adesso prendiamo in considerazione alcuni tipi particolari di equazioni logaritmiche di semplice risoluzione.
1° TIPO ( caso particolare del 1° TIPO ! )
Equazioni logaritmiche elementari riconducibili alla forma canonica:
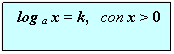
Ad esempio:
![]()
Per risolvere tali tipi elementari, supposto x > 0 per l’esistenza del logaritmo, puoi procedere in due differenti modi ma tra loro equivalenti :
§ trasformare l’equazione nell’equivalente equazione esponenziale, applicando la definizione di logaritmo, ovvero: log a x = k ↔ ak = x
§ oppure, trasformare ambo i membri dell’equazione in logaritmi di stessa base, tenendo presente la proprietà 2. dei logaritmi, e successivamente risolvere l’equazione algebrica ottenuta eguagliando gli argomenti dei logaritmi, essendo la funzione logaritmica biunivoca, ovvero:
log a x = k ↔ log a x = log a a k ↔ x = a k
Esercizi Guidati

2° TIPO ( in cui rientra anche il 1° TIPO ! )
Equazioni logaritmiche riconducibili alla forma canonica:
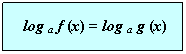
Per risolverla procediamo nel seguente modo:
§ imponiamo dapprima le condizioni di esistenza dei logaritmi, perché non esistono logaritmi di numeri negativi, ponendo quindi che ogni argomento di logaritmo contenente l’incognita x sia maggiore di zero:
![]()
§ si riconduce, eventualmente, l’equazione data nella forma canonica, applicando le proprietà dei logaritmi
§ si passa dall’equazione logaritmica alla risoluzione dell’equazione algebrica f (x) = g (x) degli argomenti, poiché da: log a f (x) = log a g (x) → f (x) = g (x)
§ si controllano se le soluzioni sono accettabili, ovvero appartengono al campo di esistenza.
Esercizi Guidati
Risolvere le seguenti equazioni riconducibili alla forma canonica: log a f (x) = log a g (x)

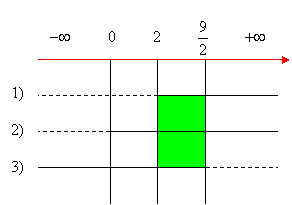
Compiliamo il quadro dei segni e prendiamo gli intervalli comuni:
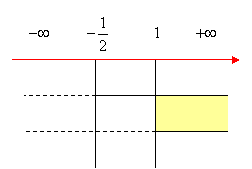
si ha dunque C.E.: x > 1


Compiliamo il quadro dei segni e prendiamo gli intervalli comuni:
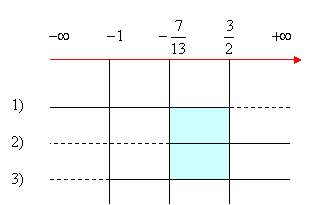

Compiliamo il quadro dei segni e prendiamo gli intervalli comuni:

3° TIPO
Prendiamo adesso in esame alcune particolari equazioni logaritmiche non riconducibili ai tipi precedentemente trattati; in tal caso si deve cercare di trasformare l’equazione in una forma del 1° Tipo mediante opportune sostituzioni, ricorrendo ad una variabile ausiliaria, ad esempio, y del tipo:
log a x = y
che trasformerà l’equazione esponenziale in un’equazione algebrica nell’incognita y, le cui soluzioni ci consentono poi di risalire alle soluzioni dell’equazione logaritmica.
Esercizi Guidati
