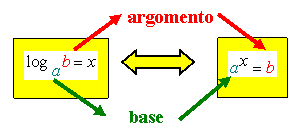
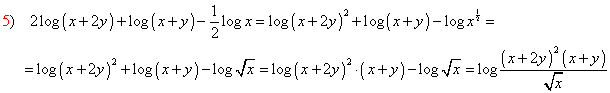Definizione di logaritmo: dati due numeri reali e positivi a e b, con a diverso da 1, si chiama logaritmo in base a di b, e si indica con log _a b, l’esponente da dare ad a per ottenere b:

Quindi il  calcolo del logaritmo in base a di b (argomento) si riconduce alla risoluzione dell’equazione esponenziale che ha per base la base a del logaritmo e per esponente x (= log_a b), vedi figura, pertanto segue che:

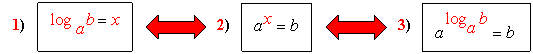
§ osservando la 1) e 2): log_a b è soluzione dell’equazione esponenziale ed è unica e sola

§ osservando la 2): il numero b (argomento del logaritmo) essendo uguale ad a^x , ovvero potenza di un numero che è sempre diversa da zero e positiva, non esistono logaritmi di numeri negativi e quindi il logaritmo esiste solo se il suo argomento è positivo

§ osservando la 3): la potenza di un numero a, positivo e diverso da 1, elevato ad un logaritmo di stessa base dà come risultato l’argomento b

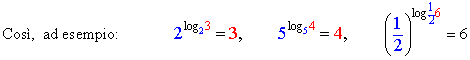
Esercizi svolti: applicazioni della definizione di logaritmo

1.  Calcoliamo i seguenti logaritmi applicando la definizione di logaritmo.

N.B.: l’incognita è x = log _a b pertanto, in base alla definizione, x è l’esponente da dare alla base a del logaritmo per ottenere l’argomento b e pertanto si riconduce alla risoluzione di un’equazione esponenziale:

2. Determinare il numero, dato il logaritmo e la base

N.B.: in questo caso l’incognita x è l’argomento e per determinarla applichiamo sempre la definizione di logaritmo;poi risolviamo l’equazione esponenziale ottenuta.

3. Determinare la base dei seguenti logaritmi

N.B.: in questo caso l’incognita x è la base e per determinarla applichiamo sempre la definizione di logaritmo; poi risolviamo l’equazione ottenuta, che come vedrai non è più esponenziale ma algebrica, perché l’esponente della potenza è un numero intero e non una incognita, e si considera come soluzione solo quella positiva dovendo essere la base x positiva.

Casi particolari:

v log_a 1 = 0, perché   a⁰ =1   per ogni a

v log_a a = 1, perché   a^a =1   per ogni a

Proprietà dei logaritmi:

v logaritmo di un prodotto:

v logaritmo di un quoto:

v logaritmo di una potenza:

I logaritmi in base 10 si indicano con log, mentre in base e ( detto numero di Nepero, irrazionale e con 2< e <3) si indica con ln

Se dobbiamo operare con logaritmi di diversa base, es. log_a b e log_c b, allora bisogna ricondurli alla stessa base, ad esempio in base c , applicando la seguente formula:

Esercizi svolti: applicazioni delle proprietà

1.  Applicando le proprietà dei logaritmi trasformare le seguenti espressioni in somme algebriche

Attenzione alla priorità delle proprietà da applicare!