Dopo la retta, che come abbiamo visto sono curve rappresentate analiticamente da equazioni algebriche di 1° grado, prendiamo in considerazione altre curve che saranno invece rappresentate analiticamente da equazioni algebriche di 2° grado.

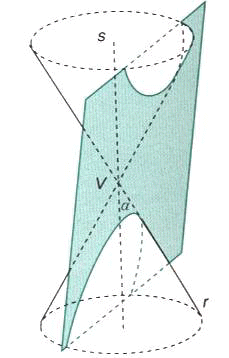
Queste curve sono dette coniche perché si ottengono sezionando con un piano la superficie di un cono indefinito a due falde, vedi figura:

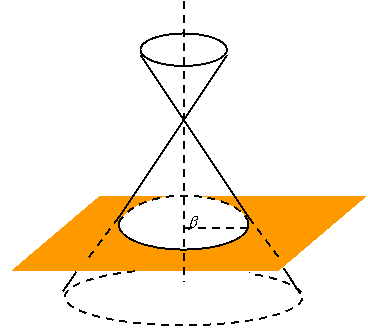
Al variare dell’ampiezza dell’angolo b formato dall’asse di rotazione della superficie conica con un piano secante si ottengono le quattro coniche:

Ø Circonferenza: nel caso particolare in cui b è retto

Ø Parabola: se b = a il piano taglia il cono lungo una sola falda

Ø Ellisse: se  b > a  il piano taglia solo una delle due falde del cono

Ø Iperbole:  se b < a  il piano taglia il cono lungo le due falde