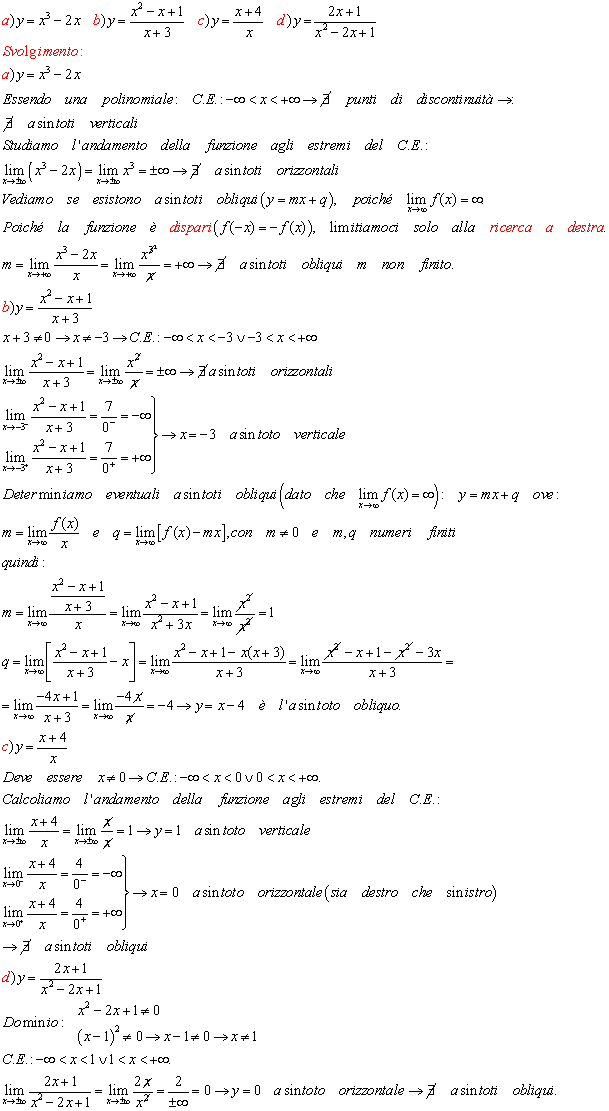Asintoti
Abbiamo avuto l’opportunità, nella ricerca del dominio di funzioni, di introdurre intuitivamente la nozione di asintoto verticale ed orizzontale del diagramma di una funzione. Adesso perveniamo a una sistematizzazione rigorosa ma semplice dei concetti di asintoti orizzontali, verticali ed obliqui, cosi detti perché non sono paralleli agli assi cartesiani, e stabiliremo, poi, alcuni metodi di ricerca degli asintoti.
Premettiamo, innanzitutto che:
f(x) può ammettere asintoti solo se la sua curva presenta un ramo che si estende all’infinito e ciò si verifica quando il suo dominio o codominio (almeno uno dei due) è illimitato.
Mediante i limiti, adesso siamo in grado di studiare ed analizzare l’andamento di una funzione nell’intorno degli estremi degli intervalli che costituiscono il suo campo di esistenza e di individuare gli asintoti.
Definizione(In generale):
Una retta si dice che è un asintoto della curva, che ha un ramo che si estende all’infinito, se la distanza tra un punto P, qualsiasi, della curva e la retta tende a zero quando P si allontana indefinitamente sulla curva, tendendo a un suo punto all’infinito.
Più semplicemente, si usa dire che:
l’asintoto è una retta tangente alla curva in un suo punto all’infinito.
Una funzione, come già detto, può avere asintoti orizzontali (cioè paralleli all’asse x), verticali (cioè paralleli all’asse y) od obliqui: essi vengono individuati mediante l’applicazione dei limiti allo studio dell’andamento della f(x) per x tendente agli estremi degli intervalli del suo campo di esistenza.
1) Ricerca degli asintoti orizzontali
Definizione: data la funzione y = f(x) se si verifica che:
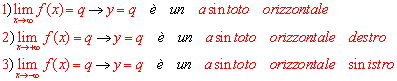
Graficamente ( gli asintoti sono stati tracciati in rosso):
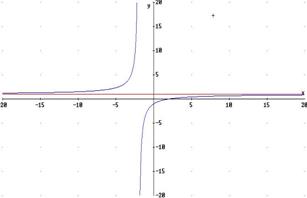
1) retta y = 1: asintoto orizzontale

2a) retta y = 1: asintoto orizzontale destro
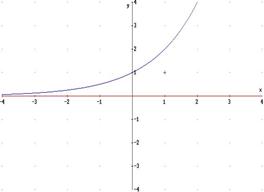
3a) retta y = 0: asintoto orizzontale sinistro
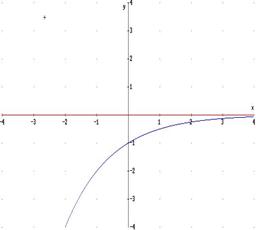
2b) retta y =0 : asintoto orizzontale destro
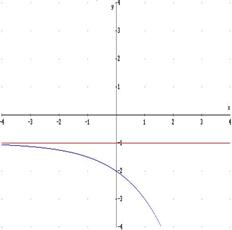
3b) retta y = -1 : asintoto orizzontale sinistro
N.B.: Esistono funzioni ( vedi grafico) il cui diagramma ammette due distinti asintoti orizzontali, purché uno destro e l’altro sinistro, altrimenti viene meno il concetto di funzione, ovvero l’univocità. Di conseguenza le funzioni periodiche non ammettono asintoti orizzontali.

2) Ricerca degli asintoti verticali
Definizione: Data la funzione y = f(x) se si verifica che:
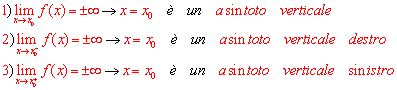
Graficamente:
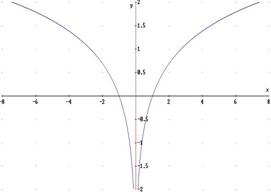
1) retta y = 0: asintoto verticale
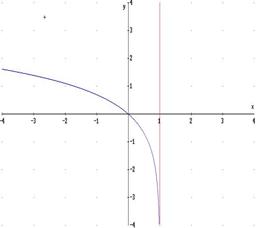
2a) retta x = 1: asintoto verticale a destra
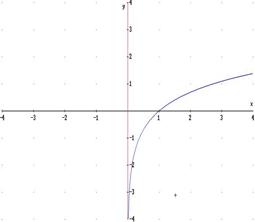
3a) retta x = 0: asintoto verticale a sinistra
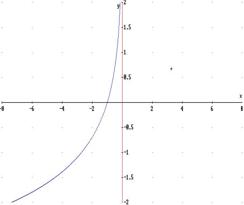
2b) retta x = 0: asintoto verticale a destra
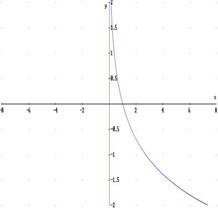
3b) retta x = 0: asintoto verticale a sinistra
N.B.:Esistono funzioni il cui diagramma ammettono infiniti asintoti verticali, basti ricordare la funzione y = tg x :
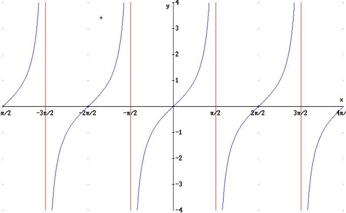
· Il diagramma di una funzione può ammettere simultaneamente asintoto orizzontale e verticale ed inoltre la curva può intersecare l’asintoto orizzontale ma non quello verticale ( vedi grafico.), in quanto quest’ultimo, come vedremo, va ricercato negli estremi (che siano punti finiti) degli intervalli del campo di esistenza:

Esercizi guidati
Determiniamo gli asintoti orizzontali e verticali delle seguenti funzioni:

 3) Ricerca degli asintoti obliqui
3) Ricerca degli asintoti obliqui
Definizione di asintoto verticale: Se un asintoto di una curva non è parallelo ad alcun asse cartesiano allora viene denominato asintoto obliquo.
Quindi
il suo modello algebrico è del tipo seguente:![]()
Pertanto per la sua determinazione occorre calcolare due limiti:

Osservazioni:
1)
Poiché per la ricerca degli
eventuali asintoti obliqui, ma anche di quelli orizzontali, deve ![]() , il dominio
della f(x) deve essere illimitato a sinistra e/o a destra:
pertanto, le funzioni aventi per dominio intervalli limitati non hanno
asintoti né orizzontali né obliqui.
, il dominio
della f(x) deve essere illimitato a sinistra e/o a destra:
pertanto, le funzioni aventi per dominio intervalli limitati non hanno
asintoti né orizzontali né obliqui.
2) Una funzione può ammettere la stessa retta come asintoto obliquo sia a destra che a sinistra della sua curva (vedi grafico):
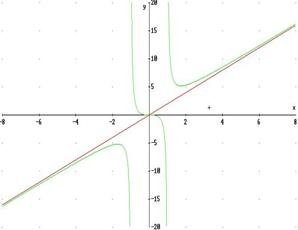
3) Una funzione può ammettere due asintoti obliqui, purché siano uno a destra e l’altro a sinistra della sua curva ( vedi grafico).Di conseguenza le funzioni periodiche non ammettono asintoti obliqui.
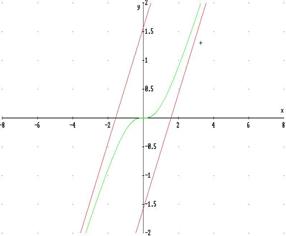
4)
Gli asintoti obliqui di
una funzione, il cui dominio sia illimitato in uno o in entrambi i sensi, si
ricercano soltanto nell’eventualità in cui ![]() .Di conseguenza , una stessa
funzione non può ammettere contemporaneamente un asintoto orizzontale e uno
obliquo dalla stessa parte (ad es. entrambi a sinistra), perché verrebbe
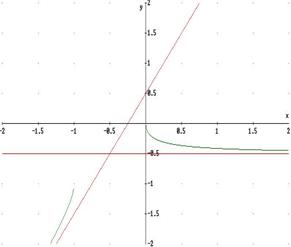
meno il concetto di funzione. Quindi una stessa curva può presentare
contemporaneamente, ad esempio, un asintoto orizzontale a destra e un asintoto
obliquo a sinistra (vedi grafico):
.Di conseguenza , una stessa
funzione non può ammettere contemporaneamente un asintoto orizzontale e uno
obliquo dalla stessa parte (ad es. entrambi a sinistra), perché verrebbe
meno il concetto di funzione. Quindi una stessa curva può presentare
contemporaneamente, ad esempio, un asintoto orizzontale a destra e un asintoto
obliquo a sinistra (vedi grafico):
Esercizi guidati
Si premette che dagli esercizi svolti e da quelli che seguiranno si deducono le seguenti:
OSSERVAZIONI
1. Le funzioni razionali intere, cioè le polinomiali, non ammettono alcun tipo di asintoto;
2. Nelle funzioni razionali fratte, cioè del tipo:A(x)/B(x):
· gli asintoti verticali vanno ricercati negli eventuali zeri del denominatore, purché non siano punti di discontinuità eliminabile
· gli asintoti orizzontali esistono se il grado di A(x) è uguale o minore al grado di B(x)
· gli asintoti obliqui esistono se il grado di A(x) supera solo di una unità il grado di B(x)
3. Le funzioni irrazionali intere non hanno asintoti verticali
4. Le funzioni goniometriche, per la loro periodicità, non presentano alcun asintoto orizzontale ed obliquo, al più possono presentare asintoti verticali
5. Nelle funzioni pari (f(-x)=f(x)), cioè simmetriche rispetto all’asse y, per la ricerca , in particolare, degli asintoti obliqui potremo ridurre notevolmente i calcoli, limitandoci a svolgere la ricerca a destra (cioè per x→∞). Infatti, se esiste l’asintoto obliquo a destra y=mx+q allora si potrà subito affermare che la curva, per simmetria, ammette anche l’asintoto sinistro y=-mx+q.
6. Analogamente per le funzioni dispari (f(-x)=-f(x)), cioè simmetriche rispetto all’asse x, ci limiteremo a svolgere la ricerca dell’asintoto a destra.Infatti, se esiste l’asintoto obliquo a destra y=mx+q allora si potrà subito affermare che la curva, per simmetria, ammette anche l’asintoto sinistro y=-mx-q.
Si consiglia di studiare il segno della f(x), perché ciò permette:
· di distinguere gli intervalli ove il diagramma della funzione è situato al di sopra o al di sotto dell’asse x
· di calcolare più dettagliatamente i limiti per x tendente all’intorno destro o sinistro di un punto estremante dell’ intervallo del C.E.
Determiniamo le equazioni degli eventuali asintoti delle seguenti funzioni razionali ed irrazionali, dopo aver determinato il dominio: