Flessi ordinari e singolari

Abbiamo già parlato di flessi orizzontali e verticali (vedi lezioni sulle derivate e crescenza-decrescenza) che richiameremo dopo aver dato la definizione generale di flesso di una curva in un punto; successivamente studieremo i flessi a tangente obliqua.

Data  una funzione, al solito, definita e continua in [a;b], insieme con le sue derivate prima e seconda, e sia x₀ un punto interno di tale intervallo, diciamo che:

la funzione presenta in x₀ un punto di flesso se nell’intorno di tale punto la curva cambia di concavità.

Osserva a tal fine i seguenti diagramma di funzioni che presentano in  x₀ un punto di flesso:

                                 fig. 5)                                                                                                 fig. 6)

Ricordiamo che:

§ se la funzione è derivabile nel punto x₀ di flesso allora esiste la tangente alla curva in tal punto e può essere orizzontale oppure obliqua, di conseguenza diremo che in x₀  la curva presenta un flesso orizzontale oppure un flesso obliquo ed in genere sono detti flessi ordinari;

§ se  la funzione non è derivabile nel punto x₀ di flesso, ossia f ‘(x) è infinita, allora la tangente è verticale, ossia parallela alle y, di conseguenza diremo che in x₀  la curva presenta un flesso verticale ed è detto flesso singolare;

§ la tangente alla curva in un suo punto di flesso, qualunque esso sia, ha la caratteristica di attraversare la curva ed inoltre il punto di tangenza è triplo come puoi notare dalla seguente figura:

§ se la curva nell’intorno del punto x₀ di flesso (orizzontale o obliquo) volge la concavità verso il basso a sinistra e verso l’alto a destra, vedi fig. 5), ossia quando la concavità, attraversando da sinistra a destra il punto, va da verso il basso a verso l’alto il flesso è ascendente;

§ se la curva nell’intorno del punto di flesso (orizzontale o obliquo) volge la concavità verso l’alto a sinistra e verso il basso a destra, vedi fig. 6),  ossia quando la concavità, attraversando da sinistra a destra il punto, va da verso l’alto a verso  il basso il flesso è discendente.

Tipi di flessi

Esistenza e ricerca di flessi

Il seguente teorema ci fornisce una condizione necessaria per l’esistenza di un flesso in un punto x₀ dell’intervallo [a;b] in cui la funzione è continua insieme alle sue derivate prima e seconda:

se f(x) ha un flesso in x₀ → f ‘’(x₀) = 0

Dimostrazione

Se per ipotesi in x₀ la curva presenta un flesso ( non verticale)allora, per definizione di flesso, nell’intorno del punto x₀ la curva nel passaggio da sinistra verso destra cambia la concavità. Pertanto proprio in x₀ né può essere f ‘’(x₀)> 0, altrimenti la curva in x₀ volgerebbe la concavità verso l’alto contro l’ipotesi, né può essere f ‘’(x₀)< 0, altrimenti la curva in x₀ volgerebbe la concavità verso il basso contro l’ipotesi, quindi l’unica conclusione è che sia f ’’(x₀ ) = 0.

Ricordiamo che il teorema è solo una condizione necessaria e quindi non invertibile.

A tal fine riportiamo il seguente:

Esempio:

Data la  funzione y = 2x⁶   definita in tutto R si ha che:

f ‘(x) =12x⁵  e f ‘’(x) = 60x⁴  → f ‘’(x) = 0,  60x⁴ =0 → x = 0

Studiamo il segno della derivata seconda:

f ‘’(x) >0, 60x⁴ >0 per ogni x ≠ 0  → la curva nell’intorno di 0 volge la concavità sempre verso l’alto.

Compiliamo il quadro dei segni della f ‘’(x):

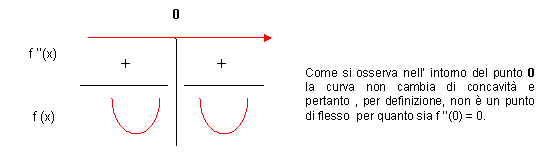
Prima di presentare l’algoritmo per la ricerca dei flessi sulla base di quanto detto precedentemente, ricordiamo che per flessi ordinari (orizzontale od obliquo) si devono intendere quei flessi che la curva presenta in punti di derivabilità per distinguerli dai flessi verticali che la curva presenta, eventualmente,  in punti di non derivabilità.

Algoritmo per la ricerca dei flessi di una curva tramite il segno della derivata seconda:

1. calcolare la derivata prima della funzione

2. calcolare la derivata seconda

3. trovare gli zeri della f ‘’(x), risolvendo f ‘’(x) = 0

4. se f ‘’(x)≠ 0 la curva non presenta flessi ordinari ( né orizzontali e né obliqui)

5. studiare il segno della f ‘’(x), cioè f ‘’(x)> 0 e di conseguenza sapremo quando è f ‘’(x)< 0, per individuare gli intervalli in cui la curva volge la concavità verso l’alto e verso il basso

6. riportare le informazioni ottenute, eventualmente, in uno schema riassuntivo per rilevare gli eventuali punti di flesso (a tangente orizzontale, se anche f ’(x₀) =0, oppure a tangente obliqua). Ricorda che tali punti si ricercano tra gli zeri della f ‘’(x) e sono quelli in cui la f ’’(x), nel passaggio da sinistra a destra di ciascuno di questi punti, cambia di segno.. A questa variazione di segno corrisponde una variazione della concavità della curva. Schematizzando, si possono presentare i seguenti due casi:

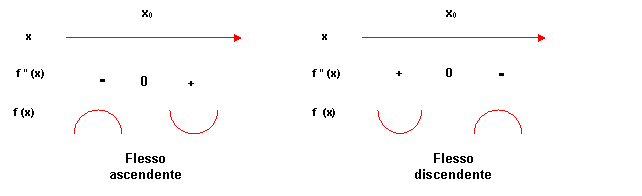
7. in quei particolari punti x₀ nei quali la funzione f(x) è continua ma non derivabile,  si hanno flessi a tangente verticale se f ‘(x₀^-) → - ∞ e f ‘(x₀⁺) → - ∞ oppure se f ‘(x₀^-) → + ∞ e f ‘(x₀⁺) → + ∞ , ossia se f ’(x) nell’intorno di x₀ tende ad infinito con lo stesso segno: in tal caso avviene un cambiamento del verso della concavità nel passaggio da sinistra verso destra del punto x₀. Infatti. schematizzando, si presentano i seguenti due casi:

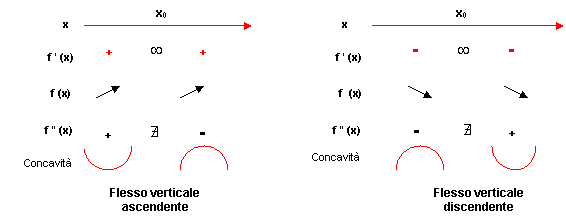
x ₀

flesso  verticale

discendente

Esercizi svolti

Calcolare i punti di flesso delle seguenti funzioni:

f ‘’(x)

f (x)

Calcoliamo l’ordinata del punto di flesso F:     f(2) = 2e^-2 → F ( 2; 2e^-2)

Compiliamo il quadro dei segni:

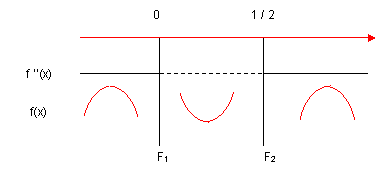
Pertanto la curva presenta due punti di flesso, precisamente: in 0, essendo f ’(0) = 0, si ha un flesso F₁ orizzontale ascendente mentre in 1/ 2 , f ’(1/2) ≠ 0, un flesso F₂ obliquo discendente.

Calcoliamo le ordinate dei punti di flesso:

f(0) = 0 → F₁(0; 0) e f(1/2)=-3/16 → F₂(1/2; -3/16).

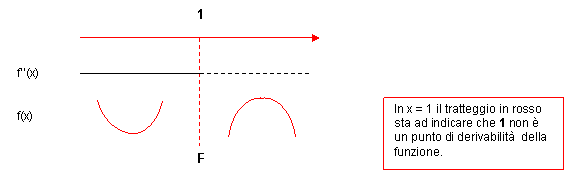
La curva cambia di concavità nell’intorno del punto 1 e pertanto si ha un punto di flesso F verticale, perché in 1 la funzione non è derivabile, ascendente perché nell’intorno sia sinistro che destro del punto 1 la f ‘(x) tende ad infinito positivo.

Calcoliamo  la sua ordinata:  f ( 1) = 0 → F(0; 1).