Per rappresentare la funzione logaritmica:

y = log _a x

riprendiamo la funzione esponenziale che come sappiamo, a secondo della base,  può avere le due seguenti curve:

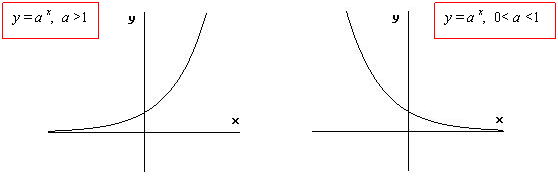
In ogni caso, si osserva che la funzione esponenziale è una funzione biunivoca, poiché ad ogni x corrisponde una ed una sola immagine y e viceversa, e quindi è invertibile ossia ammette funzione inversa e questa è propria la funzione logaritmica.

In generale, ricorda che ogni funzione continua e crescente (o decrescente) in tutto il suo dominio è invertibile.

Pertanto la curva logaritmica si ottiene da quello della funzione esponenziale, di stessa base, per simmetria rispetto alla retta  y = x, bisettrice del 1° e 3° quadrante.

In tal modo, le coordinate dei punti della curva logaritmica si ottengono da quelli della curva esponenziale scambiando in loro l’ascissa con l’ordinata, vedi figura:

Pertanto per simmetria rispetto alla bisettrice y = x  la funzione esponenziale si trasforma nella funzione logaritmica:

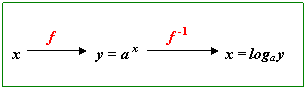
N.B.: Nulla cambia se rappresentiamo analiticamente la funzione logaritmica come  y = log_a x invece di  x = log_a y : è una questione puramente formale, dato che per consuetudine indichiamo con x la variabile indipendente e con y la variabile dipendente.

Studio della funzione logaritmica

La curva logaritmica, come quella esponenziale, varia a seconda del valore della base a:

1° Caso: a > 1

La curva logaritmica la si può anche rappresentare per punti, come abbiamo fatto per la curva esponenziale, considerando ad esempio la funzione y = log ₂ x, ottenendo il modello grafico che abbiamo precedentemente ottenuto, in modo più semplice, dalla curva esponenziale di stessa base per simmetria assiale; quindi in generale si ha:  

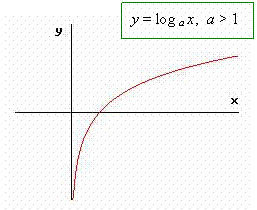
da cui si deducono le seguenti proprietà generali:

2° Caso: 0 < a < 1

La curva logaritmica, come abbiamo precedentemente visto per simmetria assiale rispetto alla curva esponenziale di stessa base, ha in generale il seguente modello grafico:

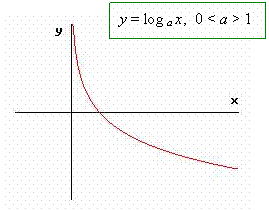
da cui si deducono le seguenti proprietà generali: