Ricerca del dominio di funzioni irrazionali

Come sappiamo, una funzione irrazionale è in generale del tipo seguente:

In essa, il radicando A(x) può essere un polinomio oppure una frazione algebrica del tipo:

Tenendo presente quanto riportato nella lezione 3 : dominio, prendiamo in esame alcuni esempi di  funzioni irrazionali.

§ Campo di esistenza delle funzioni irrazionali intere:

Determiniamo il C.E. delle seguenti funzioni, stando attenti all’indice di radice:

Svolgimento

Poiché siamo in presenza di un radicale di indice pari , la funzione data esiste in R se e solo se  si  attribuiscono alla x valori che rendono positivo o nullo il radicando, ossia che soddisfano la disequazione che si ottiene imponendo la non negatività del radicando:

Dunque, risulta che 

Interpretando graficamente tale dominio , è opportuno  eliminare quelle regioni ( in grigio) del piano dove sicuramente non si trova la curva della funzione così come segue:

N.B. : Non è stata tracciata nessuna retta parallela alla Y( in rosso: asintoto verticale)  in x = -4  e x = 4  in quanto tali punti, come abbiamo visto, appartengono al  C.E.  

Poiché l’ indice è ancora pari, il dominio della f(x) è costituito dalle soluzioni che soddisfano la seguente disequazione:

risolvendo, si ha:

Dunque:

Graficamente:

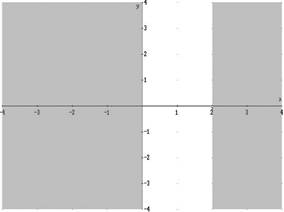
Pertanto la curva è situata interamente nella striscia di piano delimitato dalle due rette  x = 0 e  x = 2.

Poiché l’indice è ancora pari, il dominio della f(x) è costituito dalle soluzioni che soddisfano la seguente disequazione:

risolvendo l’equazione ad essa associata con la formula risolutiva o più semplicemente scomponendo il trinomio caratteristico a 1° membro , si ha:

Graficamente:

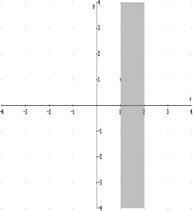
Pertanto il diagramma della funzione si decompone in due rami separati dalla striscia di piano delimita dalle due rette x =1 e x = 2.

Poiché l’indice del radicale è dispari e ricordando che esiste la radice (algebrica) di indice dispari anche dei numeri negativi , si ha che il dominio della funzione presa in esame coincide, quindi, con quello del radicando . Essendo quest’ultimo un polinomio (vedi dominio di funzioni razionali intere ), si conclude che:

La funzione in esame affinché sia definita è necessario che siano soddisfatte contemporaneamente più condizioni ed  essendo costituita da due radicali di indice pari si impone che i relativi radicandi siano non negativi, pertanto risolviamo il seguente sistema di disequazioni:

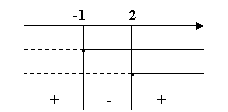
Le soluzioni comuni come si osserva dallo schema riassuntivo individuano, dunque, il

Graficamente

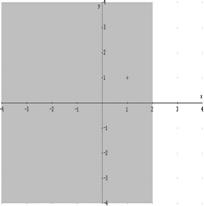
§ Campo di esistenza delle funzioni irrazionali fratte:

Determiniamo il C.E. delle seguenti funzioni, stando attenti all’indice di radice:

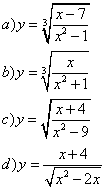
Svolgimento

La radice è d’indice dispari e pertanto il dominio coincide con quello del radicando che è una espressione razionale fratta ( vedi dominio di funzioni razionali fratte ) , dunque deve essere:

Pertanto:

Graficamente:

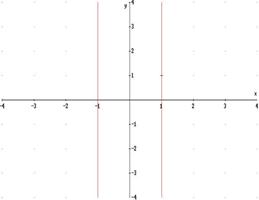
Il diagramma della funzione presenta , dunque due discontinuità nei punti x = -1 e x = 1 (in cui tracciamo in rosso due rette asintotiche verticali).

Poiché l’indice di radice è dispari, il dominio della funzione coincide con quello del radicando. Essendo quest’ultimo un’espressione razionale fratta, dobbiamo imporre che il denominatore sia diverso da zero, pertanto si ha :

Essendo l’indice di radice pari, si deve imporre per l’esistenza della funzione che sia non negativo il radicando, pertanto:

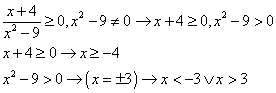
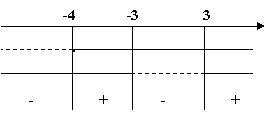
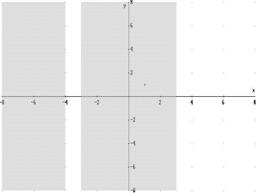
Come si osserva dallo schema riassuntivo, gli intervalli in cui f(x) è positiva costituiscono le soluzioni della disequazione fratta e pertanto:

Graficamente:

La funzione è una irrazionale con indice di radice pari  e fratta, pertanto per l’esistenza di f(x) si devono verificare contemporaneamente le due condizioni seguenti:

.

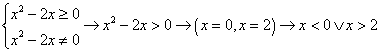
Graficamente:

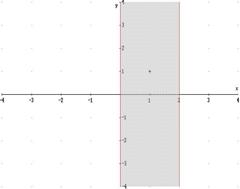
N.B.: Sono state tracciate le rette asintotiche verticali (in rosso) nei punti x = 0 e x = 2 .