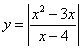Studiare e rappresentare graficamente la seguente funzione in valore assoluto:

In questi casi è opportuno dapprima studiare e rappresentare graficamente la funzione senza il valore assoluto, ovvero:
![]()
cosa che abbiamo già fatto, vedi Funzione razionale fratta.
Una volta tracciato il corrispondente grafico, si ricava immediatamente il grafico della funzione 1), in valore assoluto, considerando il simmetrico rispetto all’asse x della parte di curva situata nel semipiano negativo delle ordinate: in tal modo la curva che otterremo sarà completamente situata nel semipiano positivo delle y, ovvero la curva sarà costituita da punti aventi solo ordinate positive.
Riprendiamo, dunque, il grafico della funzione senza il valore assoluto:
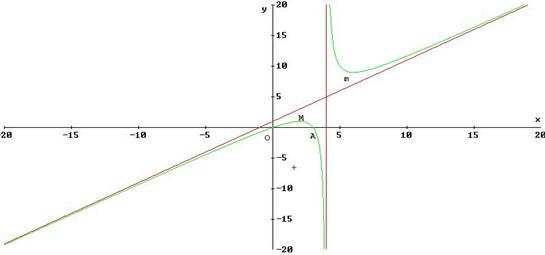
Per tracciare il grafico della funzione 1) : si riconferma della curva rappresentata la sola parte che risulta situata nel semipiano positivo delle ordinate, mentre della restante parte di curva (situata nel semipiano negativo delle y) si considera la sua simmetrica rispetto all’asse delle x. Così facendo, otteniamo il seguente diagramma:
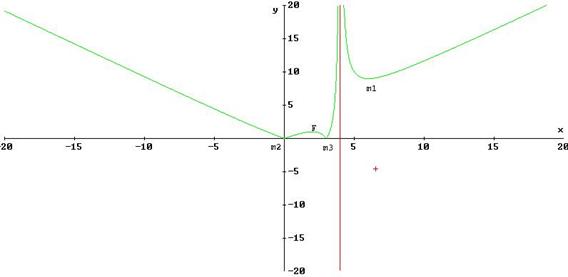
Dal grafico si deducono immediatamente le seguenti caratteristiche della curva: