Abbiamo già sentito parlare di concavità rivolta verso l’alto o verso il basso  nella rappresentazione grafica della parabola, adesso generalizziamo il concetto di concavità di una curva y = f(x) in un suo punto x₀ e pertanto trattasi di un’altra proprietà locale della funzione. Poi, attraverso il concetto di concavità daremo la nozione generale di flesso in un punto  di cui  abbiamo già parlato nel caso di flessi orizzontali e pertanto affronteremo il caso di flessi a tangente obliqua.

Data una funzione y = f(x) definita e continua in [a;b] ed ivi derivabile assieme alle sue derivate successive si dice che:

la curva, diagramma della funzione, nel P₀ volge la concavità verso l’alto se nell’intorno di quel punto la curva sta tutta al di sopra della retta tangente alla curva in P₀ (vedi fig.1) ).

Analogamente:

la curva nel P₀ volge la concavità verso il basso se nell’intorno di quel punto la curva sta tutta al di sotto della retta tangente alla curva in P₀ (vedi fig.2) )

.

fig. 1)                                                                                      fig. 2)

Si ha il seguente criterio (ossia una condizione sufficiente) per stabilire il tipo di concavità di una curva in un suo punto, correlato con il segno della derivata seconda della funzione::

Data una funzione definita e continua in [a;b], insieme con le sue derivate prima e seconda, e sia x₀ un punto appartenente a questo intervallo:

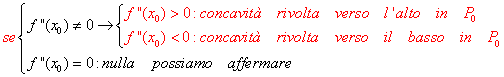
Diamo una dimostrazione geometrica del criterio.

Sappiamo che se f ‘(x₀)> 0 → f(x₀) crescente nel punto x₀, pertanto se:

f ’’(x₀)> 0 (derivata prima di f ‘(x) calcolata in x₀) → f ‘(x₀) è crescente nel punto x₀→( per il significato geometrico della derivata prima) → cresce il coefficiente angolare della retta tangente alla curva nell’intorno del punto x₀, vedi fig. 3),  questo ci consente di concludere che in P₀ la curva volge la concavità verso l’alto, perché la curva segue la direzione delle tangenti, come si voleva dimostrare.

   fig. 3)

Analogamente, sappiamo che se f ‘(x₀)< 0 → f(x) decrescente nel punto x₀, pertanto se:

f ’’(x₀)< 0 (derivata prima di f ‘(x) ) → f ‘(x₀) è decrescente nel punto x₀ → decresce il coefficiente angolare della tangente alla curva nell’intorno del punto x_0, vedi fig. 4), questo ci consente di concludere che in P₀ la curva volge la concavità verso il basso, come si voleva dimostrare.

   fig. 4)

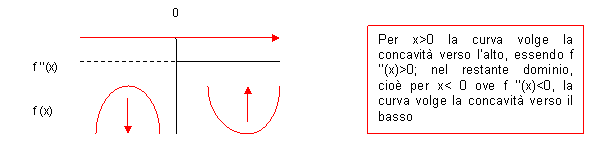
Osservazione : il teorema non è invertibile, cioè se la curva volge la concavità verso l’alto in x₀ ( verso il    

                           basso) non è detto che sia  f ‘’(x₀)>0 ( f ’’(x₀)<0 ), potrebbe infatti accadere che in tal                 

                           punto sia f ‘’(x₀ ) = 0

Basta, infatti, osservare la seguente curva:

Ricerca degli intervalli in cui una curva volge la concavità verso l’alto o verso il basso

In base al criterio precedente, per determinare tali intervalli bisogna studiare il segno della derivata seconda della funzione, ossia f ‘’(x)>0 e di conseguenza si troveranno le soluzioni di f ‘’(x)< 0.

Esempio

Determinare della seguente funzione:       y = f(x) = 2x³ - 5

gli intervalli in cui il grafico della funzione volge la concavità verso l’alto o verso il basso.

Innanzitutto la funzione è definita in tutto R.

Calcoliamo la derivata prima e seconda di f(x) nel generico punto x:  f ‘(x) = 6x² ,      f ’’(x) = 12x

Studiamo il segno della derivata seconda, ossia f ’’(x) > 0:     12x > 0 → x > 0

Compiliamo il quadro relativo allo studio del segno della derivata seconda: