Date due funzioni f(x) e g(x) continue in un intorno Ix₀ - { x₀ } tali che:

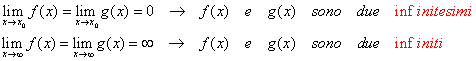
Confrontare  due infinitesimi oppure due infiniti significa stabilire chi delle due funzioni considerate tende più rapidamente a 0 oppure a ∞  o se tendano a 0 oppure a ∞  con la stessa rapidità.

Per effettuare tale confronto basta calcolare il limite del rapporto delle due funzioni infinitesime o infinite.

Precisamente:

Per calcolare il limite del rapporto di due funzioni che si presenta nelle due forme indeterminate: 0/0 e ∞/∞, per ovviare alle difficoltà di calcolo che comporta tale limite con le tecniche precedentemente utilizzate, (vedi lezione sul calcolo di limite in forme indeterminate) possiamo, se le funzioni sono derivabili, applicare la regola di De L’Hospital:

In pratica sostituiamo il limite del rapporto di due funzioni derivabili che si presenta nelle forme indeterminate 0/0 oppure ∞/∞ con quello delle loro derivate: geometricamente, significa stabilire la rapidità della curva  con cui tende a 0 oppure a ∞  attraverso la velocità istantanea (o derivata) della funzione in un punto che, come sappiamo, è uguale al coefficiente angolare della retta tangente alla curva in quel punto.

Vediamo attraverso alcuni esempi come procedere per confrontare tra loro due infinitesimi o due infiniti :