Continuità e discontinuità delle funzioni.

Definizione: Una funzione f(x) ,  definita nel dominio D, è:

Una funzione è continua in [a, b] se è continua in ogni punto di questo intervallo.

Più semplicemente: una funzione è continua se tracciamo con un unico tratto  la sua curva senza staccare la penna dal foglio; es. di funzione continua è la funzione esponenziale , che è continua in ogni punto x di R.:

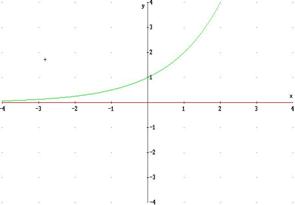
Le funzioni sono continue in tutti i punti appartenenti al loro dominio D.

Se non si verifica una sola delle tre condizioni di continuità della f(x), sopra citate, allora si dice che la funzione non  è continua in , oppure che , (punto di accumulazione per D), è un punto di discontinuità per f(x): in tal caso,  come ad es. per la funzione  y = tag x , la curva non si può tracciare con un unico tratto di penna, in quanto in corrispondenza dei punti , nei quali non è definita,  subisce delle interruzioni:

fig. 1)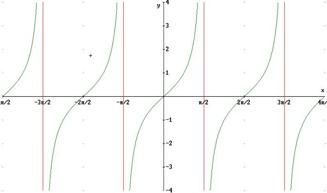

Precisamente, le funzioni possono presentare tre tipi di discontinuità:

1. Discontinuità di 1^a  specie: quando in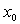esistono finiti il limite destro e sinistro della f(x) ma tali limiti sono diversi tra di loro, ossia:

La differenza dei due limiti prende il nome di salto della funzione in.Vedi fig.2)

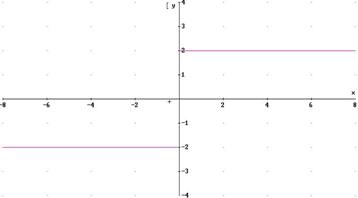
                                  fig.2)

2. Discontinuità di 2^a specie: quando in 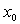si verifica una delle seguenti eventualità :

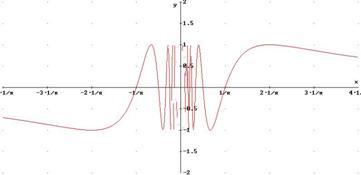
                                   fig.3)

3. Discontinuità di 3^a  specie ( o eliminabile): quando esiste finito il limite  ma la funzione non è definita in

Esercizi guidati

a) Stabilire la continuità delle seguenti funzioni nei punti  a fianco indicati:

b) Determinare i punti di discontinuità delle seguenti funzioni: