Correlazione tra funzione crescente e decrescente e il segno della sua derivata prima

Funzioni crescenti e decrescenti in un intervallo chiuso e limitato

Premetto che quando parliamo di funzioni crescenti o decrescenti senza precisare altro, intendiamo considerare funzioni crescenti o decrescenti  in senso stretto. Ciò significa che dobbiamo considerare la relazione < oppure > e non  ≥  oppure  ≤ , che invece si considerano per le funzioni crescenti o decrescenti in senso lato  che definiremo in seguito.

Una funzione f(x) è crescente in un intervallo se e solo se al crescere delle ascisse crescono le corrispondenti ordinate, ossia se:

x₁< x₂  → f(x₁ ) < f(x₂)

Quindi nelle funzioni crescenti ad incrementi positivi della x corrispondono incrementi della y dello stesso e quindi positivi, ovvero i rapporti incrementali  ∆y/∆x sono sempre positivi.

[Nel caso in cui  risulti:

x₁< x₂  → f(x₁ ) ≤ f(x₂)

allora la funzione si dice non decrescente (o crescente in senso lato), cioè  f(x) o cresce o si mantiene costante].

Osserviamo attentamente il diagramma di due funzioni crescenti (in senso stretto):

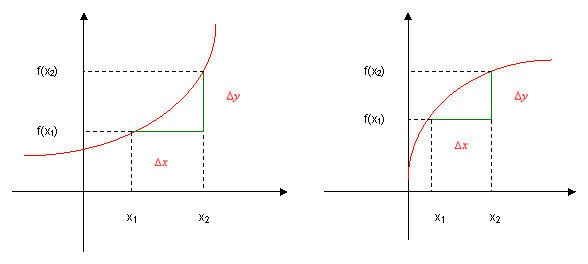
fig. 1a)                                                                                     fig. 1b)

Una funzione f(x) è decrescente in un intervallo se e solo se al crescere delle ascisse decrescono le corrispondenti ordinate, ossia se:

x₁< x₂  → f(x₁ )> f(x₂)

Pertanto nelle funzioni decrescenti ad incrementi della x corrispondono decrementi della y, quindi i rapporti incrementali sono sempre negativi

[Nel caso in cui  risulti:

x₁< x₂  → f(x₁ ) ≥ f(x₂)

la funzione si dice non crescente (o decrescente in senso lato), ovvero la f(x) o decresce o si mantiene   

costante]

Osserviamo attentamente i diagrammi di due funzioni decrescenti in senso stretto:

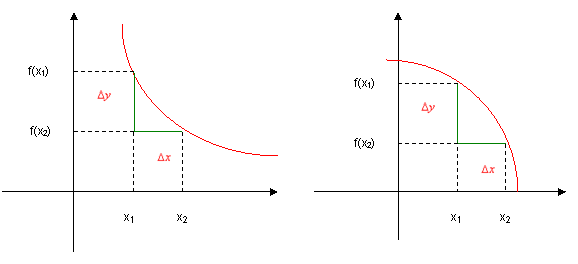
fig. 2a)                                                                                       fig. 2b)

Ebbene, se una funzione continua e derivabile ha derivata f ’(x) > 0  in tutti i punti dell’intervallo (aperto o chiuso) di definizione ciò comporta, per definizione di derivata, che il limite del rapporto incrementale è positivo e, per il teorema della permanenza del segno, che anche il rapporto incrementale è positivo, che come sappiamo è una caratteristica delle funzioni crescenti.  

Pertanto, possiamo dire che:

1. se risulta  f ’(x) > 0  in tutti i punti di [a;b]  allora la funzione è crescente in [a;b]

Invece, se una funzione continua e derivabile ha derivata f ’(x) < 0  in tutti i punti dell’intervallo (aperto o chiuso) di definizione ciò comporta, per definizione di derivata, che il limite del rapporto incrementale è negativo e, per il teorema della permanenza del segno, che anche il rapporto incrementale è negativo, che come sappiamo è una caratteristica delle funzioni crescenti.  

Pertanto, possiamo dire che:

2. se risulta  f ’(x) < 0  in tutti i punti di [a;b]  allora la funzione è decrescente in [a;b]

Non è vero il viceversa , ossia:

se la funzione è crescente o decrescente in [a;b] allora non è detto che sia f ’(x)> 0  o f ‘ (x)< 0

Infatti basta considerare come esempio il diagramma delle funzioni rappresentate in fig. 3a) e fig. 3b):

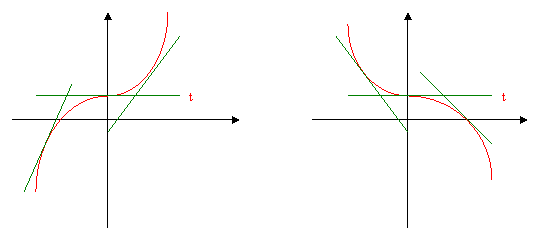
               fig. 3a)                                                                                 fig. 3b)

Infatti, come si osserva in fig. 3a) le tangenti ad una curva con andamento strettamente crescente  o hanno coefficiente angolare m>0 ( perché formano con l’asse delle x un angolo acuto)  o m = 0 (perché la retta tangente t  è parallela all’asse delle x) e pertanto, tenuto conto dell’interpretazione geometrica della derivata prima di una funzione in un punto x generico dell’intervallo di definizione, si ha che in tali punti risultano rispettivamente f ’(x) > 0 oppure f ’(x) = 0.

Analogamente, dal grafico illustrato in fig. 3 b) si rileva che se  la funzione  ha andamento decrescente la condizione f ’(x)< 0 non risulta verificata in tutti i punti x interni all’intervallo di definizione. Infatti la tangente t nel punto x = 0  ha coefficiente angolare m = 0 e quindi  f ’(x) = 0.

Pertanto, possiamo affermare che:

se f(x) è crescente (o decrescente) → f ’(x) ≥ 0  ( o f ’(x) ≤ 0 )

Come vedremo meglio in seguito, il punto nell’intorno del quale la funzione è crescente (o decrescente) e derivata nulla viene denominato flesso a tangente orizzontale ( vedi fig. 3) e 3b).

Funzioni crescenti e decrescenti in un punto

Come è stata definita la funzione crescente e decrescente nell’intervallo [a;b], cioè globalmente, allo stesso modo si definisce la funzione crescente e decrescente in un punto x₀ interno ad [a;b]. Solo che questa volta non si tratta di una proprietà globale ma di una proprietà locale della f(x), ossia di una proprietà valida soltanto in un opportuno intorno del punto x₀.

Infatti, una funzione si dice crescente o decrescente nel punto x₀ se e soltanto se in un intorno completo di x₀, (x₀ - h ; x₀ + h) contenuto in [a; b], si verificano rispettivamente le seguenti implicazioni:

se  ( x₀ - h < x₀ < x₀ + h) → f(x₀ – h) < f(x₀) < f(x₀ + h)

oppure

se  ( x₀ - h < x₀ < x₀ + h) → f(x₀ – h) > f(x₀) > f(x₀ + h)

Osservazione

Per determinare, dunque, gli intervalli in cui una funzione è crescente o decrescente basta studiare il segno della sua derivata prima.

Esempio

Determinare in quali intervalli è crescente o decrescente la seguente funzione

y =x³-3x²+1

Innanzitutto determiniamo il dominio: la funzione è definita per ogni x reale.

Per determinare in quali intervalli la f(x) è crescente o decrescente studiamo il segno della sua derivata prima che è la seguente:

y ‘ = 3x²-6x

Studiamo y’ > 0:

3x²-6x > 0 →  x²-2x > 0 → x(x-2) >0 → ( x = 0 , x = 2) → x< 0 V x>2

Compiliamo il quadro dei segni:

In corrispondenza degli intervalli con segno positivo, tracciamo la freccia rivolta verso l’alto per indicare che la funzione è crescente; in corrispondenza di quelli con segno negativo tracciamo la freccia rivolta verso il basso per indicare che la funzione è decrescente

Quindi la funzione è crescente per x< 0 V x>2 mentre è decrescente nel restante intervallo, cioè per 0<x<2.