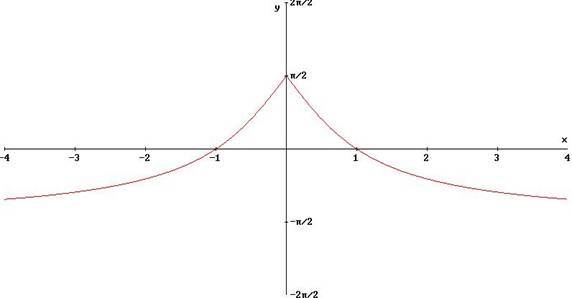
Studio di funzione goniometrica inversa

Premessa

Ricordiamo che  le funzioni goniometriche seno, coseno e tangente non sono invertibili in tutto il loro dominio, perché in esso non risultano, vedi  lezione “Le funzioni trascendenti” (in “ Le funzioni: proprietà globali e locali”) sempre crescenti o decrescenti. Però risultano invertibili, e quindi ammettono la funzione inversa, solo a tratti o meglio in quei intervalli del loro dominio in cui esse sono solo o monotone crescenti o monotone decrescenti.

Precisamente:

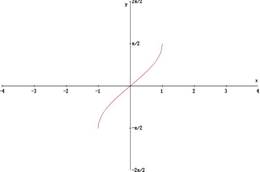
§ la funzione seno in [-π/2; π/2] risulta sempre crescente: in tale intervallo dunque ammette la funzione inversa,  arcoseno e pertanto il codominio [-1;1] della funzione seno definita in tale intervallo s’invertirà nel dominio della funzione arcoseno, i cui corrispondenti valori y, ossia il codominio che indicheremo con C_d, sarà invece [-π/2; π/2] , quindi :                                       

y = arcsin x  →  C.E.: -1 ≤  x ≤ 1 e  C_d: -π/2≤  y ≤ π/2

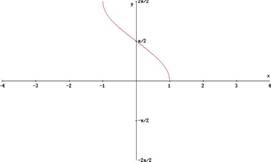
§ la funzione coseno in [0; π] risulta sempre decrescente: in tale intervallo dunque ammette la funzione inversa, arcocoseno; quindi, facendo lo stesso ragionamento fatto precedentemente, si ha.

y = arccos x  →  C.E.: -1 ≤  x ≤ 1 e  C_d: 0 ≤  y ≤ π

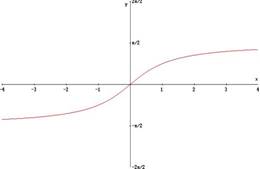
§ la funzione tangente in [-π/2; π/2] risulta sempre crescente: in tale intervallo dunque ammette la funzione inversa,  arcotangente e pertanto il dominio e codominio della funzione tangente s’invertirà rispettivamente in codominio e dominio della funzione arcotangente, ossia:

y = arctg x  →  C.E.: -∞< x <+∞  e  C_d: -π/2≤  y ≤ π/2