Punti stazionari: massimi, minimi e flessi orizzontali

Definiamo dapprima massimi e minimi relativi di una funzione detti anche locali perché riguardano proprietà valide soltanto in un opportuno intorno di un punto del dominio della funzione; poi definiremo massimi e minimi assoluti detti anche globali perché riguardano proprietà valide in tutto il dominio della funzione.

Una funzione definita in un certo intervallo aperto o chiuso si dice che presenta in x₀ un punto di massimo relativo ( o locale) se esiste un intorno I_o di  x₀  tale che  f(x₀) sia maggiore o uguale del valore che la funzione assume in qualsiasi altro punto dell’intorno I_o , ossia:

Una funzione definita in un certo intervallo aperto o chiuso si dice che presenta in x₀ un punto di minimo relativo ( o locale) se esiste un intorno I_o di  x₀  tale che  f(x₀) sia minore o uguale del valore che la funzione assume in qualsiasi altro punto dell’intorno I_o , ossia:

Una funzione ammette un massimo assoluto (o globale) M in un intervallo [a;b] di definizione  se M è maggiore o uguale del valore che la funzione assume in qualsiasi altro punto di [a;b] . ossia:

Una funzione ammette un minimo assoluto (o globale) m in un intervallo [a;b] di definizione  se m è minore o uguale del valore che la funzione assume in qualsiasi altro punto di [a;b] . ossia:

Osserva attentamente il diagramma seguente:

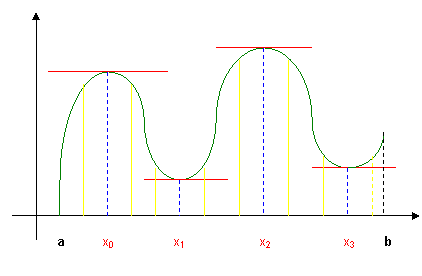
fig. 1)

Come puoi notare in un punto di massimo relativo, in x₀ e in x₂, la funzione attraversando da sinistra verso destra l’ intorno del punto x₀ e x₂,  (contrassegnato da segmenti in giallo) cambia andamento: risulta crescente nell’ intorno sinistro dei punti, essendo f ‘(x)>0;  poi stazionaria nel punto x₀ e x₂, poiché  f ‘(x₀) = f ‘(x₂) = 0 essendo in tali punti di massimo relativo le tangenti sono parallele all’asse delle x; infine è  decrescente nell’intorno sinistro, essendo f ‘(x)< 0.

Anche nei punti di minimo relativo, in x₁ e in x_3, la funzione  attraversando da sinistra verso destra l’intorno del punto (contrassegnati da segmenti in giallo) cambia andamento: però risulta decrescente nell’intorno sinistro di x₁ e x₃, essendo f ‘(x)< 0; poi diventa stazionaria in x₁ e in x₃, cioè f ‘(x₁)=f ‘(x₃)=0   perché anche in tali punti di minimo relativo le tangenti sono parallele all’asse delle x, ed infine è  crescente nell’intorno sinistro, essendo f ‘(x)> 0.

Inoltre, confrontando i punti estremanti, cioè i punti di massimo e di minimo relativo, e i valori assunti da f(x) agli estremi dell’intervallo chiuso di definizione, osserviamo che il diagramma della curva presenta in [a;b] un massimo assoluto coincidente con il massimo relativo in x₂, e un minimo assoluto coincidente con il valore f(a) estremo sinistro di [a;b].

Questo sta a significare che il massimo o il minimo assoluto assunto in un intervallo chiuso e limitato coincide con quelli relativi o eventualmente con i valori che la funzione assume agli estremi dell’ intervallo.

Ricordiamo che:

§ Se la funzione è continua e definita in un intervallo chiuso e limitato ammette senz’altro un massimo o un minimo assoluto (teorema di Weierstrass).

§ Non sempre una funzione è dotata di estremi assoluti.

Infatti, se la funzione è definita in un intervallo aperto non si può determinare in modo finito il valore assunto dalla funzione agli estremi dell’intervallo e pertanto non può avere un massimo o un minimo assoluto, perché ricordiamo che il massimo assoluto e il minimo assoluto oltre ad essere rispettivamente la massima e la minima ordinata assunta dalla funzione nel suo dominio devono essere finite e appartenenti al codominio della funzione.

§ I punti di massimo e di minimo relativo, di una funzione derivabile, si ricercano nei punti in cui in cui si annulla la sua derivata prima, cioè f ‘(x) = 0  è condizione necessaria per l’esistenza dei punti di massimo o di minimo relativo in un punto interno all’intervallo.

Infatti, geometricamente abbiamo visto, fig. 1), che nei punti estremanti, massimi e minimi, relativi la tangente è parallela all’asse x  quindi se x₀  è un punto stremante  risulta f ‘ (x₀) = 0.

Non è vero il viceversa, cioè se f ‘ (x₀) = 0 non è detto che in x₀ ci sia un punto di Max o di min relativo.

Infatti, osservando i diagramma seguenti:

fig. 2a)                                                                       fig.2b)

si può notare come nei punti x₀ la retta tangente ai grafici delle funzioni per quanto siano parallele  all’asse delle x non c’è né un punto di massimo né di minimo relativo. Infatti, osserva la fig. 2a), la funzione attraversando l’intorno del punto x₀ sia a sinistra che a destra è sempre crescente oppure, come in fig. 2b), è sempre decrescente: la funzione, dunque, attraversando l’intorno di x₀ non cambia andamento come avviene nei punti di massimo o di minimo relativi. In tal caso si dirà che la funzione presenta in x₀ un punto di flesso a tangente orizzontale (ascendente nel primo caso, discendente nel secondo).

Algoritmo: per la ricerca dei punti di massimo, minimo relativi e flessi orizzontali mediante il         

                   segno della derivata

Premettiamo che i punti di massimo, minimo relativi e flessi orizzontali si ricercano nei punti in cui la funzione è derivabile  ma anche non derivabile, ovvero dove risulta discontinua òla f’(x) ; in quest’ultimo caso saremo in presenza di punti critici (vedi lezione sulle DERIVATE). A prescindere da qualsiasi ipotesi di derivabilità e non derivabilità della funzione seguiremo i seguenti passi per determinare i punti estremanti e flessi orizzontali:

1) Calcolare la derivata prima f ‘(x) della funzione (e vedere  se esiste in tutto il C.E. della funzione data per individuare la presenza di eventuali punti critici)

2) Determinare gli zeri della derivata prima: f ‘(x)=0 , così facendo si determinano i punti stazionari; in caso non esista alcun zero allora la funzione non ha alcun punto di Max, min relativi e flesso orizzontale

3) Studiare il segno della derivata prima: f ‘(x)>0, così facendo determiniamo gli intervalli in cui la funzione è crescente e, quindi, nei restanti intervalli risulterà decrescente

4) Riportare in un schema riassuntivo tutte le informazioni trovate e rilevare gli eventuali punti di massimo o minimo relativo o flesso orizzontale, ricordando che:

• x₀  è un punto di massimo relativo se la funzione è crescente nell’intorno sinistro di x₀  e decrescente nell’intorno destro di x₀)

• x₀  è un punto di minimo relativo se la funzione è decrescente (f ’(x)<0) nell’intorno sinistro di x₀ e crescente(f ’(x)>0)  nell’intorno destro di x₀

• x₀ è un punto di flesso a tangente orizzontale se la funzione risulta crescente sia a destra che a sinistra dell’intorno del punto, per cui si ha un flesso ascendente; oppure se la funzione  risulta decrescente sia a destra che a sinistra nell’intorno del punto in tale intorno pertanto il flesso è discendente)

             Schema riassuntivo:

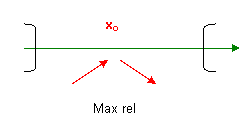
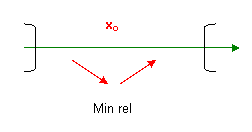
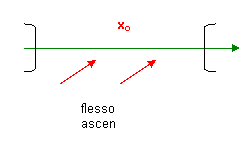
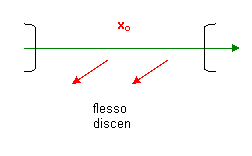
5) Ricercare, utilizzando sempre lo stesso algoritmo, eventualmente punti di Max e min relativi in punti di non derivabilità della funzione derivata f ‘(x) ma che sono punti appartenenti al dominio della funzione data e, come sappiamo, sono punti critici ( vedi ultimo esempio 3)).

Esempi

Determinare i punti stazionari delle seguenti funzioni:

1)y = x³ - 3x

La funzione è definita in tutto R.

Calcoliamo la derivata prima:

y ‘= 3x² – 3

che è definita anch’essa in tutto R.

poniamo y ‘ = 0 per la ricerca dei punti stremanti:

3x² – 3 = 0 →x² – 1 = 0 →x = ± 1

Studiamo adesso il segno della derivata prima, y ‘ >0 :

3x² – 3>0 → x² – 1>0 → x< -1 V x> 1

Compiliamo il quadro dei segni: riportando i punti in cui si annulla la derivata prima e ponendo negli intervalli in cui la derivata è positiva la freccia rivolta verso l’alto, che sta ad indicare la crescenza della funzione,  e negli intervalli in cui la derivata è negativa la freccia verso il basso, che sta ad indicare la decrescenza della funzione:

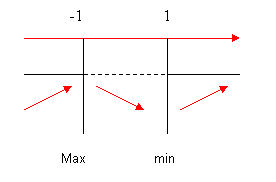
Come si osserva la f(x) attraversando i punti ± 1 cambia andamento quindi si tratta di punti di Max e di min relativi e precisamente:

in x = -1 si ha un punto di massimo relativo, ben visibile nel quadro, poiché la f(x) ha andamento crescente nell’intorno sinistro e poi decrescente nell’intorno destro;

in x = 1 si ha un punto di minimo relativo poiché la f(x) ha andamento decrescente nell’intorno sinistro e poi crescente nell’intorno destro.

Calcoliamo le ordinate dei punti stremanti:

f (- 1 ) = -1 + 3 = 2 → M (- 1;  2)

f( -1 ) = 1 – 3 = - 2→ m (1; - 2).

La funzione essendo definita in un aperto non ha né Max né min assoluti.

Funzione definita in tutto R, calcoliamo la derivata prima:

y ‘ = x² - 2x + 1

che è definita anch’essa in tutto R.

y’ = 0 per

x²-2x + 1 = 0 → ( x - 1)² = 0 → x -1=0 → x = 1

Studiamo il segno della funzione, y ‘ >0:

 ( x - 1)² > 0   ¥ x ≠ 1

Compiliamo il quadro dei segni:

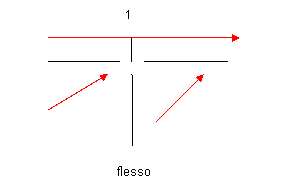
Come si osserva la funzione nell’intorno del punto x = 1 non cambia andamento e precisamente è sempre crescente, quindi in x = 1 si ha un flesso ascendente a tangente orizzontale.

Calcoliamo l’ordinata del flesso :

La funzione essendo definita in un aperto non ha né Max né min assoluti.

Compiliamo lo schema riassuntivo, riportando tutte le informazioni trovate: C.E., il punto di non derivabiltà, crescenza e decrescenza della funzione ( e nel caso ci fossero stati anche i punti stremanti ordinari):

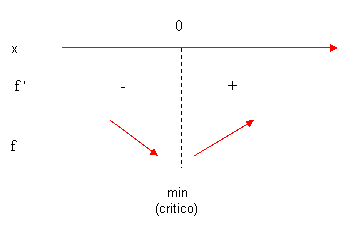
Come abbiamo visto la funzione non ha punti di Max e min ordinari ma dallo schema si rileva un minimo relativo nel punto di non derivabilità che denota una cuspide rivolta verso il basso.

Inoltre la funzione non ha Max o min assoluti perché definita in un aperto.