Grafico e caratteristiche della funzione seno: la sinusoide

fig. 1

y = sen x

Grafico e caratteristiche della funzione coseno: la cosinusoide

fig. 2

y = cos x

Grafico e caratteristiche della funzione tangente: la tangentoide

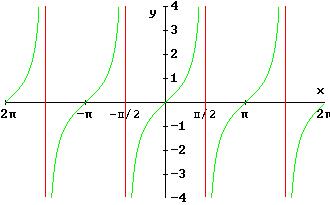fig. 3

y = tg x

Le funzioni goniometriche inverse

Le funzioni goniometriche seno, coseno e tangente non sono invertibili in tutto il loro dominio (cioè non ammettono la funzione inversa in tutto il loro dominio, come la funzione esponenziale e logaritmica)  perché nei relativi domini o le funzioni come seno e coseno, pur essendo continue, non risultano sempre crescenti o decrescenti, o perché come la funzione tangente pur avendo rami sempre crescenti non è però continua.

Però, risultano invertibili, e quindi ammettono la funzione inversa, solo a tratti o meglio in intervalli ristretti del loro dominio in cui esse risultano solo o monotone crescenti o monotone decrescenti.

Precisamente:

§ la funzione seno in [-π/2; π/2], vedi fig.1, risulta sempre crescente: in tale intervallo dunque ammette la funzione inversa detta arcoseno, la cui rappresentazione grafica la si ottiene dunque da quella della funzione seno, relativamente al suddetto intervallo, per simmetria rispetto alla bisettrice del 1° e 3° quadrante. Pertanto, per ottenere il dominio e condominio della funzione inversa basta invertire la x con la y della funzione seno, ovvero: il codominio [-1;1] della funzione seno definita in [-π/2; π/2] s’invertirà nel dominio della funzione arcoseno; mentre il dominio ristretto [-π/2; π/2] della funzione seno s’invertirà nel condominio della funzione arcoseno, che indicheremo con C_d, quindi: 

y = arcsen x  →  C.E.: -1 ≤  x ≤ 1  e  C_d: -π/2≤  y ≤ π/2

quindi invertendo l’asse x con l’asse y, il grafico della funzione  y = arcsenx  è :

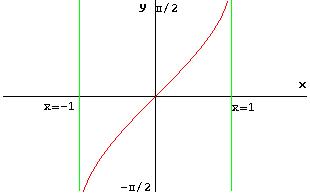
§ la funzione coseno in [0; π] risulta sempre decrescente: in tale intervallo dunque ammette la funzione inversa, arcocoseno; quindi, facendo lo stesso ragionamento fatto precedentemente per la funzione arcoseno, si ha.

y = arccos x  →  C.E.: -1 ≤  x ≤ 1  e  C_d: 0 ≤  y ≤ π

quindi invertendo l’asse x con l’asse y, il grafico della funzione  y = arccosenx  è:

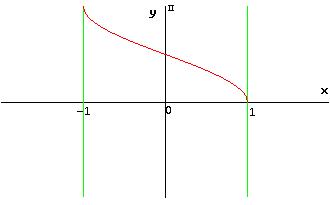
§ la funzione tangente in (-π/2; π/2) risulta sempre crescente e continua: in tale intervallo dunque ammette la funzione inversa,  arcotangente e pertanto il dominio e codominio della funzione tangente s’invertirà rispettivamente in codominio e dominio della funzione arcotangente, ossia:

y = arctg x → C.E.: -∞<  x <+∞  e  C_d: -π/2≤  y ≤ π/2

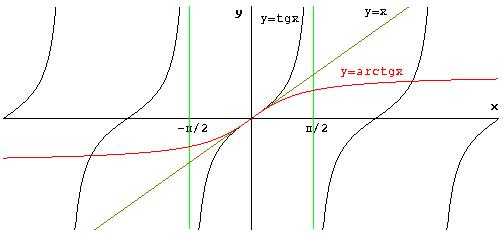
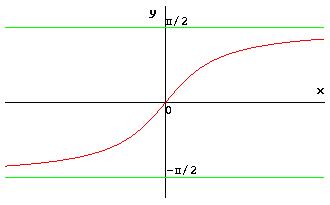
quindi invertendo l’asse x con l’asse y, il grafico della funzione  y = arctgx  è:

Riepilogando: