Quando ci proponiamo di determinare il valore a cui “tende”, ovvero a cui “ si avvicina”,  una funzione y = f(x) quando facciamo “tendere” (“avvicinare”) la x ad un punto c, appartenente o no al suo dominio D, vuol dire, in termini specifici, calcolare il limite l della funzione f(x) per x tendente a c. 

Quindi, quando per  x → c ( x tende a c),  f(x) → l  ( f(x) tende a l) scriveremo in simboli:

Intuitivamente, possiamo dire che: dando alla x valori sempre più vicini a c,  f(x) assume valori sempre più prossimi a l.

Il concetto generale di limite di una funzione, come definiremo più avanti in modo rigoroso, si baserà sulle relazioni di appartenenza a determinati intorni di punti di accumulazione e pertanto, per la comprensione, è bene venir a conoscenza di alcuni elementi di Topologia come premessa ai limiti.

Ricordiamo, innanzitutto, che il limite di una funzione y = f(x) è uno strumento matematico che ci consente di descrivere una proprietà locale, precisamente il comportamento di una funzione nell’intorno, ossia nelle vicinanze, di un punto c, che sia di accumulazione per il dominio di f(x).

Evidentemente, se il punto c appartiene al dominio di f(x) esiste il corrispondente valore f(c) assunto dalla funzione in c; se invece c non appartiene al dominio tale valore non esiste.

Si fa presente, però, che non interessa conoscere il valore assunto dalla f(x) nel punto c, che potrebbe anche non appartenere al dominio della funzione, ma soltanto quelli che essa assume in prossimità di esso; quindi il concetto di limite è indipendente dal comportamento della funzione nel punto c.

Premesso ciò, sia y = f(x) una funzione definita in un certo dominio D e c un punto di accumulazione per D. Il punto c quindi può appartenere oppure no al dominio.

Definizione Generale del concetto di limite: Si dice che la funzione f(x) tende al limite l (finito o infinito) per x tendente a c (finito o infinito) e si scrive:

se preso un qualsiasi intorno I_l di l esiste in corrispondenza un intorno I_c di c tale che per ogni x appartenente all’intorno I_c , contenuto nel dominio D di f(x), con x diverso da c, risulta sempre che il corrispondente valore f(x) appartiene all’intorno I_l, ovvero:

Tutte le definizioni ricalcano lo stesso schema, differenziandosi per il fatto di considerare intorni finiti o dell’infinito, come vedremo in seguito nei vari casi di limiti di funzione.

Limite finito per x che tende ad un numero finito

Si dice che la funzione f(x) per x tendente a c ha per limite il numero finito l (o tende a l ) e si scrive

( e si legge “limite per x che tende a c di  f(x) è uguale a l” )

se preso (sull’asse y) un qualunque intorno I_l circolare di centro l e raggio ε > 0 quantità molto piccola a piacere, ovvero (l – ε; l + ε), in corrispondenza ad esso possiamo determinare (sull’asse x), un intorno completo I_c del punto c, contenuto nel dominio D della funzione, tale che per tutti gli x appartenenti a I_c , diversi da c, i corrispondenti valori f(x) cadono all’interno di I_l (ossia, le immagini f(x) risultano comprese tra gli estremi dell’intervallo (l – ε; l + ε)):                                    

l – ε < f(x) < l + ε

che possiamo scrivere come                  

Interpretazione grafica:

Osservazioni

· La disuguaglianza  sta a significare che, man mano diamo alla x valori sempre più vicini a c, f(x) assume valori sempre più prossimi a l, da differire da l ancor meno di una quantità ε piccola quanto si vuole, per cui possiamo dire che il valore a cui tende f(x) nell’intorno di c è proprio l.

· Ricordati che la seguente disuguaglianza:

      Come vedremo, nella verifica di limite, si  risolverà  la 1) o la 2),  secondo il modello della funzione.

· L’intorno I_l di l non deve essere necessariamente circolare, è solo per semplicità di calcolo che lo prendiamo tale ed inoltre non deve essere necessariamente completo come nei casi di limite destro o sinistro, che come vedremo in seguito, graficamente, basterebbe che I_l sia un intorno destro o sinistro; quindi il fatto che I_l sia completo e circolare è solo per semplificare i calcoli nelle verifiche di limite. Generalmente, indichiamo con ε il raggio di  I_l e con δ il raggio di I_c, dipendente da ε.

· Si fa presente che tale definizione non permette operativamente di determinare il limite di una funzione, ma soltanto di verificare se un dato valore è effettivamente il limite oppure no.

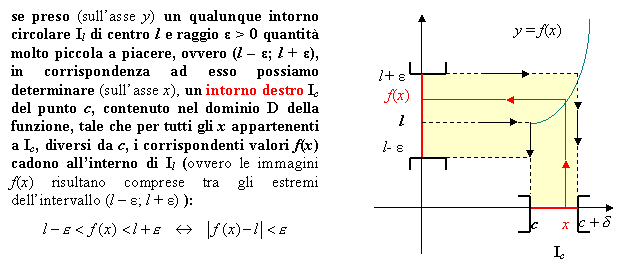
Limite destro

Quando si considerano solo valori di x appartenenti a un intorno destro del punto c, si parla di limite destro della funzione nel punto c e viene indicato con il simbolo

si legge “per x che tende a c da destra” e sta ad indicare che x si avvicina a c restando però sempre maggiore di c.

La definizione è analoga a quella generale, solo che questa volta in corrispondenza dell’intorno di I_l  si deve determinare un intorno destro di c del tipo ]c; c + δ[ con δ dipendente da ε .Ovvero:

Si dice che la funzione f(x) per x tendente a c ha per limite destro il numero finito l

Limite sinistro

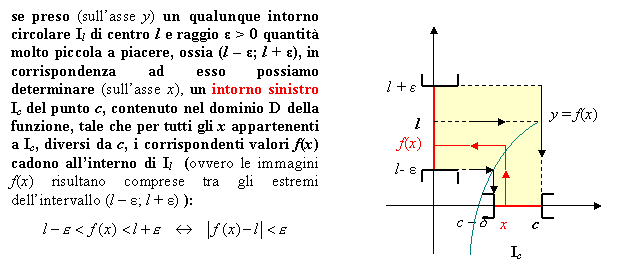
Analogamente si può parlare di limite sinistro di una funzione e viene indicato con il simbolo

si legge “per x che tende a c da sinistra” e sta ad indicare che x si avvicina a c restando però sempre minore di c.

La definizione del limite sinistro è analoga a quella del limite destro, solo che questa volta in corrispondenza dell’intorno di I_l si deve determinare un intorno sinistro di c  del tipo ] c - δ; c [ con δ dipendente da ε .Ovvero:

Si dice che la funzione f(x) per x tendente a c dalla sinistra ha per limite sinistro il numero finito l (o tende a l ) e si scrive

Osservazioni

· In generale, si considera il limite destro o il limite sinistro di una funzione quando questa non è definita nell’intorno completo del punto c. Così, ad es., non ha senso considerare il limite di  per x che tende a 0 dato che la funzione è definita per  ma possiamo calcolare il suo limite per x che tende a 0⁺.

· Se i limiti destro e sinistro di una funzione y = f(x) per x che tende a c sono coincidenti  allora possiamo dire che la funzione ha limite per x tendente a c e   viceversa, ovvero:

· Se i limiti destro e sinistro non sono coincidenti, non è possibile pervenire ad un’espressione unificante i due limiti, allora la f(x) non ha limite  per x tendente a c . Ad esempio, consideriamo la seguente funzione definita da una doppia legge:

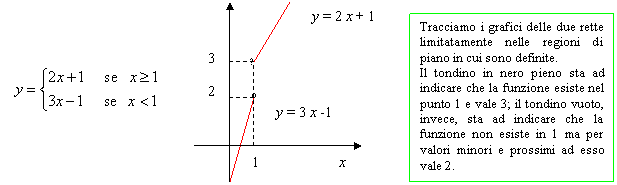
Come si osserva, anche dalla figura, non possiamo per questa funzione considerare il limite per x che tende a 1, perché la funzione è definita dalla legge y = 2 x + 1 solo per valori di x ≥1, mentre è definita da un’altra legge  y = 3 x - 1 solo per valori di  x < 1; quindi la funzione non è definita nell’intorno completo del punto 1 e pertanto possiamo prendere in considerazione solo i limiti destro e sinistro:

Poiché i due limiti non sono uguali allora non esiste il limite della funzione per x che tende a 1.

Applicazioni pratiche: verifica di limite utilizzando la definizione

In generale, per verificare che

· fissato un qualsiasi numero ε reale e positivo si pone I f(x) – l I < ε

· si esplicita il valore assoluto scrivendo:   - ε <  f(x) – l  < ε   →  l - ε <  f(x)  <  l  +  ε

· si calcola l’insieme S delle soluzioni risolvendo il seguente sistema equivalente alla precedente disequazione:

· se si verifica se tra le soluzioni (tenendo però in considerazione il dominio di  f(x)) esiste almeno un intorno completo di c, tipo ] c – δ; c + δ[ con δ in funzione di ε, o ciò che è lo stesso troviamo gli ; in tal caso l è proprio il limite della funzione per x → c

· se x → c⁺ allora tra le soluzioni dobbiamo trovare un intorno destro di c, ossia gli x > c + δ; se x → c^-  invece tra le soluzioni dobbiamo trovare un intorno sinistro di c, ossia gli x < c - δ

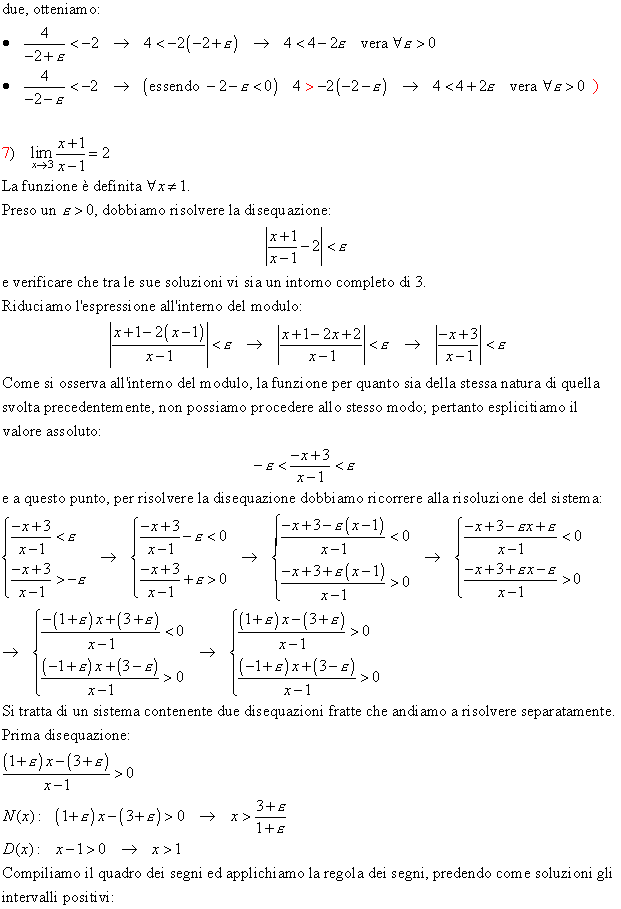
Esercizi svolti (Stai attento al modello della funzione e al suo dominio!)

Applicando la definizione di limite, verificare che:

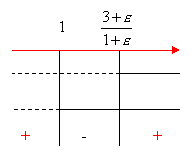
Compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

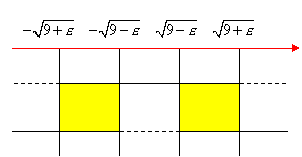
Compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

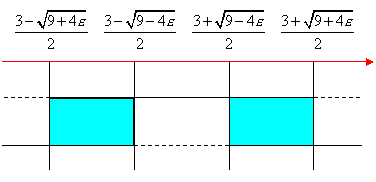
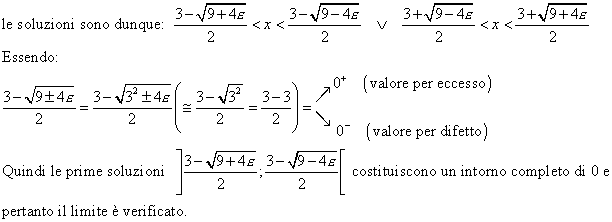
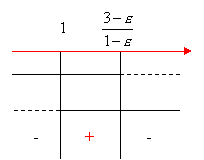
Per determinare le soluzioni del sistema, compiliamo il quadro dei segni riportando le soluzioni delle due disequazioni fratte e prendendo le soluzioni comuni:

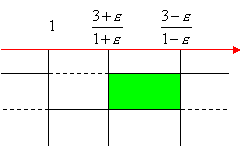
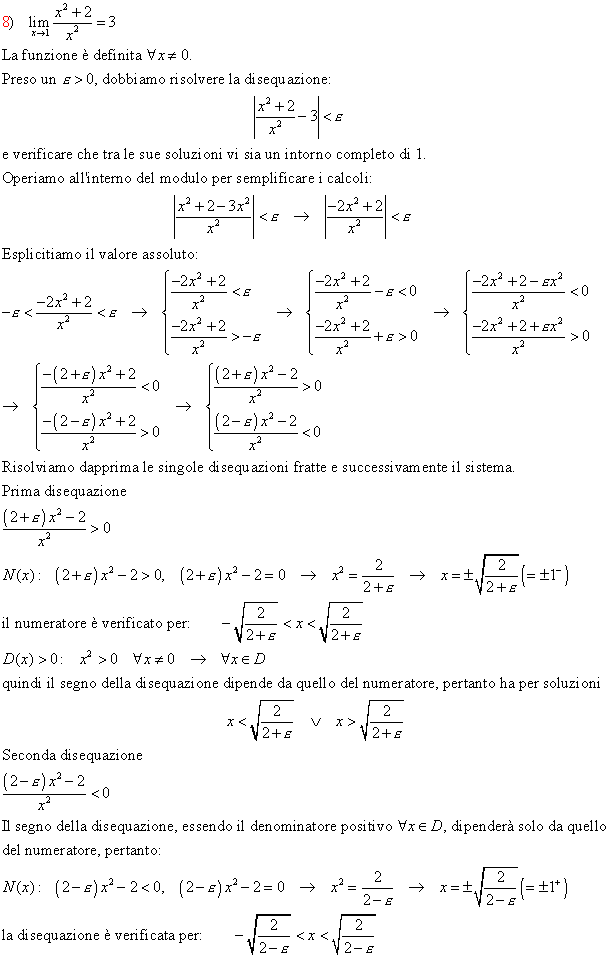
Compiliamo il quadro dei segni e prediamo le soluzioni comuni:

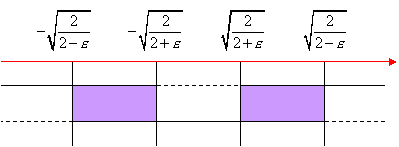
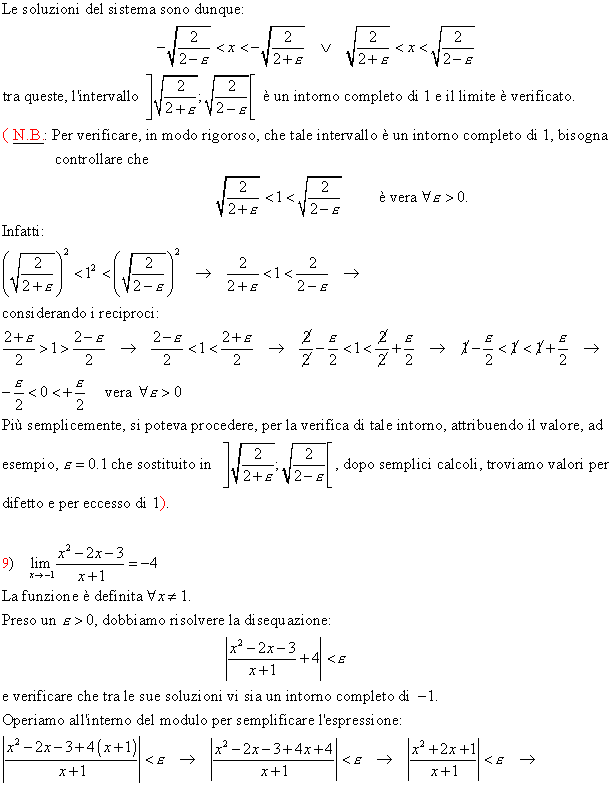
Compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

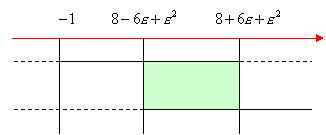
Compiliamo il quadro dei segni e prendiamo le soluzioni comuni:

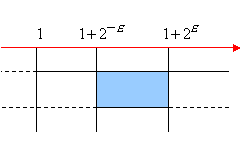
Il limite dunque è verificato.