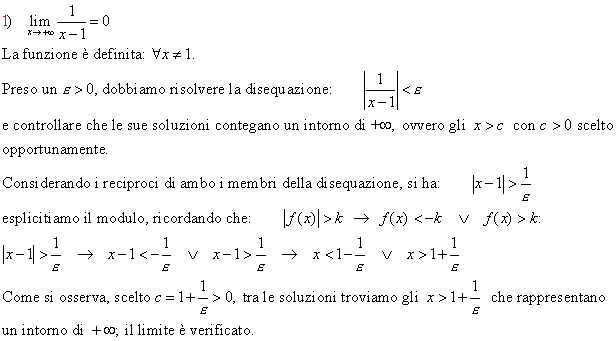Sia y = f(x) una funzione definita in un certo intervallo D illimitato, cosicché la variabile x può tendere all’infinito.

1. Limite finito per x che tende a più infinito

Si dice che la funzione f(x) ha per limite il numero finito l per x tendente a  + ∞ e si scrive

(intuitivamente: quando dando alla x valori sempre più grandi,  f(x) assume valori sempre più prossimi a l )

se preso (sull’asse y) un qualunque intorno circolare I_l di l e raggio  quantità molto piccola a piacere, ovvero , in corrispondenza ad esso possiamo determinare (sull’asse x), un intorno I_+∞ di + ∞, ovvero un punto c > 0 tale che per tutti gli x > c il corrispondente valore  f(x) cade all’interno di I_l , cioè  f(x) risulta compresa tra gli estremi dell’intervallo  :

Interpretazione grafica:

Applicazioni pratiche: verifica di limite utilizzando la definizione

In generale, per verificare che

· fissato un qualsiasi numero ε reale e positivo si pone I f(x) – l I < ε

· si esplicita il valore assoluto scrivendo:   - ε <  f(x) – l  < ε   →  l - ε <  f(x)  <  l  +  ε

· si calcola l’insieme S delle soluzioni risolvendo il seguente sistema:

· si controlla se le soluzioni (tenendo in considerazione il dominio di f(x)) contengano almeno un intorno di  + ∞, ovvero gli  x > c  con c > 0  scelto opportunamente.

2. Limite finito per x che tende a meno infinito

Si dice che la funzione f(x) ha per limite il numero finito l per x tendente a  - ∞ e si scrive

(intuitivamente: quando dando alla x valori sempre più piccoli,  f(x) assume valori sempre più prossimi a l )

Applicazioni pratiche: verifica di limite utilizzando la definizione

In generale, per verificare che

· fissato un qualsiasi numero ε reale e positivo  si pone I f(x) – l I < ε

· si esplicita il valore assoluto scrivendo:   - ε <  f(x) – l  < ε   →  l - ε <  f(x)  <  l  +  ε

· si calcola l’insieme S delle soluzioni risolvendo il seguente sistema:

· si controlla se le soluzioni (tenendo presente il dominio di f(x)) contengano almeno un intorno di - ∞, ovvero gli  x < - c con  - c < 0 scelto opportunamente.

3. Limite finito per x che tende a infinito (senza segno)

Si dice che la funzione f(x) ha per limite il numero finito l per x tendente a  ∞ e si scrive

Osservazioni

· Scrivendo x → ∞ si intende che i valori di x tendono sia a - ∞ che a + ∞, cioè

· Se si ha , come si osserva dalla fig.1, i punti del grafico di f(x), al crescere di x, tendono ad avvicinarsi sempre più alla retta  y = l . Si dice allora che la retta y = l  è un asintoto orizzontale destro del grafico di f(x).

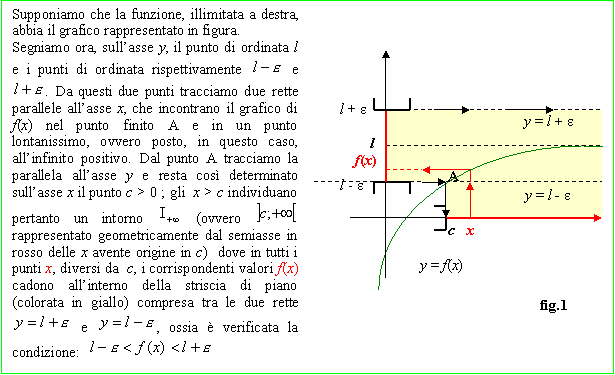
Analogamente, se si ha , come si osserva dalla fig.2, i punti del grafico di f(x), al decrescere di x, tendono ad avvicinarsi sempre più alla retta  y = l . Si dice allora che la retta y = l  è un asintoto orizzontale sinistro del grafico di f(x).

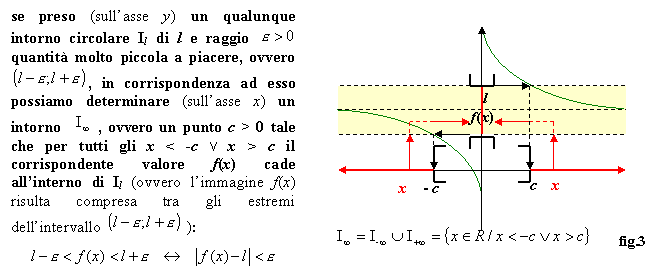
Infine, se è , vedi fig.3, allora la retta y = l  è un asintoto orizzontale sia destro che sinistro del grafico di f(x) e in tal caso si dirà semplicemente asintoto orizzontale.

Applicazioni pratiche: verifica di limite utilizzando la definizione

In generale, per verificare che

· fissato un qualsiasi numero ε reale e positivo  si pone I f(x) – l I < ε

· si esplicita il valore assoluto scrivendo:   - ε <  f(x) – l  < ε   →  l - ε <  f(x)  <  l  +  ε

· si calcola l’insieme S delle soluzioni risolvendo il seguente sistema:

· si controlla se le soluzioni (tenendo presente il dominio di f(x)) contengano un intorno di  ∞, ovvero gli  x < - c v x > c  , con  c > 0 scelto opportunamente.

Esercizi svolti

Applicando la definizione di limite, verificare che: