1. Limite più infinito per x che tende ad un numero finito

Si dice che la funzione f(x) per x tendente a c ha per limite + ∞ e si scrive

(intuitivamente: se per valori di x che si avvicinano a c i corrispondenti valori della funzione       f(x) crescono sempre più)

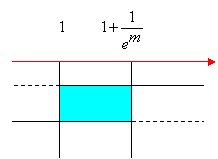
se preso (sull’asse y) un qualunque intorno I_+∞ di +∞, del tipo  y > m  con m un numero reale molto grande a piacere, in corrispondenza ad esso possiamo determinare (sull’asse x), un intorno completo I_c del punto c, contenuto nel dominio D di f(x), tale che per tutti gli x appartenenti a I_c, diversi da c, i corrispondenti valori f(x) cadono all’interno di I_{+ ∞} (ossia, le immagini f(x) risultano ancor più grandi di  m ):                                                                         

f(x) > m

Interpretazione grafica:

2. Limite meno infinito per x che tende ad un numero finito

Si dice che la funzione f(x) per x tendente a c ha per limite - ∞ e si scrive

(intuitivamente: se per valori di x che si avvicinano a c i corrispondenti valori della funzione   f(x) decrescono sempre più)

3. Limite infinito per x che tende ad un numero finito

Si dice che la funzione f(x) per x tendente a c ha per limite  ∞ e si scrive

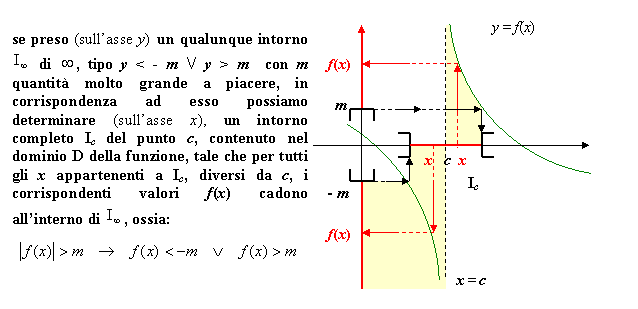
Osservazione

Se f(x) non è definita in c e  allora la retta x = c parallela all’asse delle y tangente al grafico della curva all’infinito prende il nome di asintoto verticale, in particolare:

Applicazioni pratiche: verifica di limite utilizzando la definizione

1. In generale, per verificare che   :

· fissato a piacere numero reale m molto grande  si pone:

f(x) > m

· si determinano le soluzioni della disequazione

· si controlla se le soluzioni (tenendo in considerazione il dominio di f(x)) contengano un intorno completo di c di ampiezza dipendente da m, ovvero gli  con  in funzione di m

2. In generale, per verificare che   : 

· fissato a piacere numero reale m molto grande  si pone:

f(x) < - m

· si determinano le soluzioni della disequazione

· si controlla se le soluzioni (tenendo in considerazione il dominio di f(x)) contengano un intorno completo di c di ampiezza dipendente da m, ovvero gli  con  in funzione di m

3. In generale, per verificare che  :

· fissato a piacere numero reale m molto grande  si pone:

· si determinano le soluzioni della disequazione

· si controlla se le soluzioni (tenendo in considerazione il dominio di f(x)) contengano un intorno completo di c di ampiezza dipendente da m, ovvero gli  con  in funzione di m.

Esercizi svolti

Applicando la definizione di limite, verificare che: