1. Limite più infinito per x che tende a più infinito

Si dice che la funzione f(x) per x tendente a + ∞  ha per limite + ∞ e si scrive

(intuitivamente: se per valori crescenti di x crescono sempre più i corrispondenti valori  f(x))

se preso (sull’asse y) un qualunque intorno  di , del tipo  y > m  con m un numero reale molto grande a piacere, in corrispondenza ad esso possiamo determinare (sull’asse x), un intorno  di, contenuto nel dominio D della funzione, ovvero un punto c > 0 tale che per tutti gli x > c i corrispondenti valori f(x) cadono all’interno di I_{+ ∞} (ovvero, le immagini f(x) risultano ancor più grandi di  m):      f(x) > m

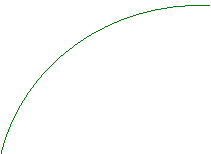
Interpretazione grafica:

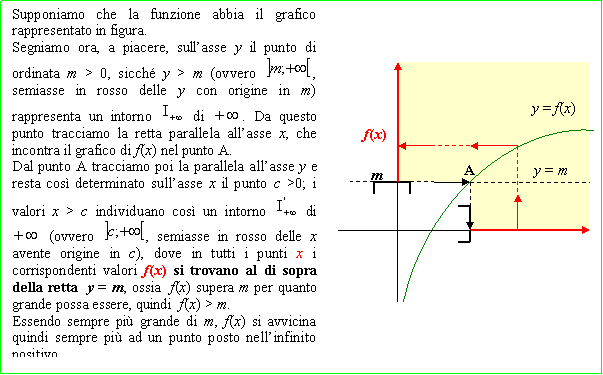
2. Limite più infinito per x che tende a meno infinito

Si dice che la funzione f(x) per x tendente a - ∞  ha per limite + ∞ e si scrive

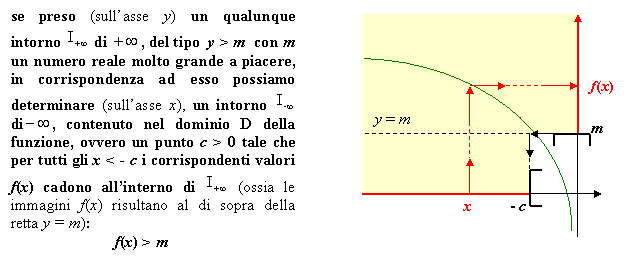
3. Limite meno infinito per x che tende a più infinito

Si dice che la funzione f(x) per x tendente a +∞  ha per limite - ∞ e si scrive

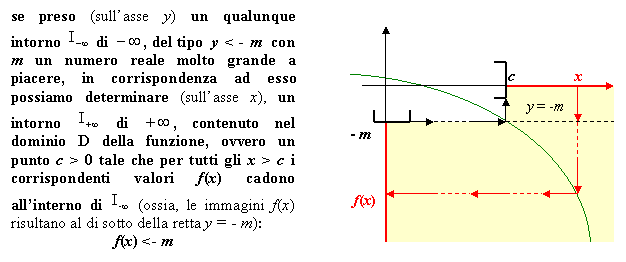
4. Limite meno infinito per x che tende a meno infinito

Si dice che la funzione f(x) per x tendente a - ∞  ha per limite - ∞ e si scrive