Ricordiamo i tre modi ( a) algebrico, b) insiemistico e c) geometrico) con cui possiamo rappresentare un intervallo aperto di estremi a e b ( estremi esclusi):

Intorni di un punto

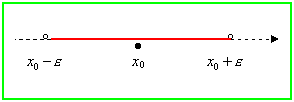
Dato un numero reale o un punto x_o, si chiama intorno completo di x_o un qualunque intervallo aperto contenente x₀:

e che rappresenteremo geometricamente con

Esempi:

· ]0;2[ è un intorno circolare del punto x₀ = 1 di raggio uguale a 1, perché 1 rappresenta il punto medio del segmento di estremi 0 e 2,  ovvero

· ]5-2; 5+2[ = ]3;7[  è l’intorno circolare di 5 di raggio uguale a 2

In generale, chiameremo:

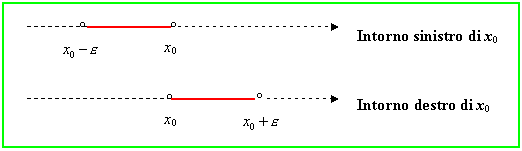
· intorno sinistro di x₀  l’intervallo:

· intorno destro di x₀  l’intervallo:

· intorno di  un qualsiasi intervallo illimitato del tipo:

· intorno di  un qualsiasi intervallo illimitato del tipo:

· intorno di  l’unione tra un intorno di meno infinito e un intorno di più infinito:

N.B.:  x < - M V x > M  è equivalente a

Punto di accumulazione

Dato un insieme I di punti, sottoinsieme di R, e x₀ un punto appartenente o no ad I, si dice che x₀ è un punto di accumulazione dell’insieme I se i suoi punti si avvicinano indefinitamente a x₀ , ovvero se ogni intorno completo di x₀ contiene infiniti punti di I.

· ogni punto di un intervallo è di accumulazione per l’intervallo stesso

· gli estremi di un intervallo sono suoi punti di accumulazione

Esempio

Sia I = ]2;4[ , il punto 3 appartenente ad I è di accumulazione per I perché ogni intorno di 3 contiene infiniti punti di I; anche i punti 2 e 4, che non appartengono ad I, sono di accumulazione per I .