Il limite di una funzione in una variabile reale è stato definito a partire da alcuni concetti topologici relativi ai punti di una retta quali: intorni, punti di accumulazione, di frontiera…
Analogamente, per comprendere il concetto di limite di una funzione in due variabili è necessario conoscere alcuni dei concetti topologici relativi ai punti del piano.
Estendiamo, adesso, le definizioni date per le funzioni di una variabile, con semplici modifiche, alle funzioni di due variabili.
Data la funzione di due variabili z = f(x, y), indichiamo con P(x,y) un generico punto del suo dominio D e con Po(xo, yo) un punto di accumulazione per il dominio.
v Limite finito
La funzione z = f(x, y) tende al limite l, per P tendente a Po e si scriverà:
![]()
se preso un
numero positivo![]() ,
arbitrariamente piccolo, si può determinare in corrispondenza ad esso un
intorno circolare di Po, tale che per ogni punto P di questo intorno,
diverso al più da Po, si abbia:
,
arbitrariamente piccolo, si può determinare in corrispondenza ad esso un
intorno circolare di Po, tale che per ogni punto P di questo intorno,
diverso al più da Po, si abbia:
![]()
v Limite infinito
La funzione z = f(x, y), definita in un insieme illimitato D, ammette limite infinito, per P tendente a Po e si scriverà:
![]()
se preso un numero positivo M, arbitrariamente grande, si può determinare in corrispondenza ad esso un intorno circolare di Po, tale che per ogni punto P di questo intorno, diverso al più da Po, si abbia:
![]()
In modo analogo si definiscono le
altre due definizioni di limite finito e infinito per ![]() . Inoltre, per i limiti di
funzioni in due variabili si possono estendere, con opportune modifiche
formali, gli stessi teoremi dei limiti di funzione di una variabile:
l’unicità del limite, la permanenza del segno, il confronto dei limiti e le
operazioni con i limiti.
. Inoltre, per i limiti di
funzioni in due variabili si possono estendere, con opportune modifiche
formali, gli stessi teoremi dei limiti di funzione di una variabile:
l’unicità del limite, la permanenza del segno, il confronto dei limiti e le
operazioni con i limiti.
v Esistenza del limite
Ricordati, però, che per una funzione di una variabile, un intorno è in realtà un segmento. Infatti, per stabilire a quale limite tende la funzione quando la x tende a c, punto di accumulazione, facciamo “avvicinare” la x al punto c, per valori prossimi in un suo intorno, da due soli versi, da sinistra e da destra:
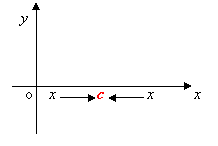
E solo quando il limite destro e il limite sinistro esistono e sono coincidenti allora possiamo dire che esiste il limite della funzione nel punto c.
Invece, per una funzione in due variabili, l’intorno circolare di un punto Po(xo, yo) è un cerchio nel piano Oxy e quindi quando facciamo tendere il punto P(x,y) al punto Po, di accumulazione per il dominio, significa che P si può “avvicinare” al centro Po di tale intorno circolare in modi diversi, ossia da una qualunque direzione e non secondo una direzione prestabilita. Ad esempio, si può pensare che P si avvicini a Po, senza mai toccarlo, percorrendo un tratto di retta o di un’altra curva qualunque passante per Po oppure che P “giri” intorno a Po lungo una curva a spirale; motivo questo, per cui tale limite è detto anche limite superficiale:
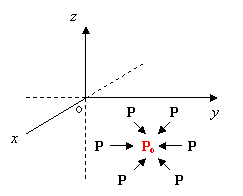
Proprio per questo motivo, a differenza delle funzioni di una sola variabile, per le funzioni in due variabili non ha più senso parlare di limite destro e di limite sinistro.
Però, è intuitivamente evidente, per analogia all’esistenza del limite di una funzione in una variabile, che il limite finito o infinito di una funzione in due variabili esiste solo se esistono e sono uguali i limiti qualunque sia il percorso con cui si faccia tendere P a Po, perché, come abbiamo detto, P può “avvicinarsi” a Po secondo una qualsiasi direzione, ad esempio, lungo una retta o lungo una curva del piano Oxy passante per Po. Però:
Ø se lungo una curva qualsiasi la funzione non ammette limite possiamo concludere dicendo che non esiste il limite della funzione
Ø se lungo una curva la funzione ammette limite non possiamo concludere che esiste il limite della funzione, perché per esistere la funzione deve ammettere lo stesso limite lungo un’altra qualsiasi curva.
Esercizio guidato
Stabilire se esiste il seguente limite:
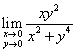
Innanzitutto la funzione è definita in tutto R2-{(0,0)} e O(0,0) è punto di accumulazione per il suo dominio. Proviamo a vedere se esiste tale limite quando facciamo tendere un punto generico del dominio P(x, y) a O(0,0) lungo la parabola x = y2 che passa per l’origine O; andiamo dunque a sostituire y2 nella x della funzione, ottenendo:
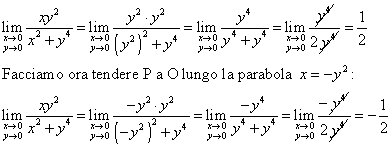
Come si osserva i due limiti sono distinti e quindi possiamo concludere che non esiste il limite della funzione nel punto O .
Vediamo, adesso, cosa accade se facciamo tendere P a O lungo la retta generica passante per l’origine y = mx, sostituendo si ottiene:
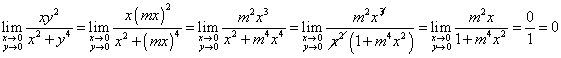
Quindi, qualunque sia il coefficiente della retta per O, la funzione ammette sempre lo stesso limite che vale zero. Però, possiamo solo dire che la funzione ammette limite nel punto O solo lungo la direzione delle rette per O e non che esiste il limite della funzione dato che, come abbiamo verificato, lungo le parabole per O non esiste il limite.
Ø Per stabilire in modo più agevole l’esistenza del limite di una funzione per P che tende a Po oppure per calcolare il limite che si presenta nella forma di indecisione, ricorriamo alle coordinate polari.
Si supponga di calcolare il limite:
![]()
Considerato un sistema di riferimento polare, con polo in Po(xo, yo) e asse polare parallelo all’asse x:
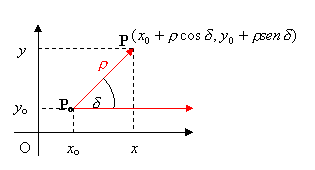
Si hanno le seguenti relazioni intercorrenti tra le coordinate polari ![]() e le coordinate
cartesiane x e y:
e le coordinate
cartesiane x e y:
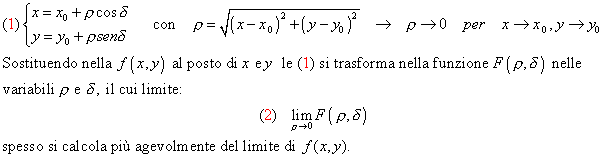
Osservazioni:
Ø
se il limite (2) dovesse dipendere
da ![]() , ovvero
varia al variare dell’angolo, allora il limite di f(x, y) evidentemente
non esiste perché non è unico;
, ovvero
varia al variare dell’angolo, allora il limite di f(x, y) evidentemente
non esiste perché non è unico;
Ø
se invece il limite esiste indipendentemente da ![]() allora il limite di f(x,
y) potrebbe esistere, perché in realtà per essere certi dell’esistenza
del limite bisognerebbe, in base ad un teorema, verificare che la funzione
allora il limite di f(x,
y) potrebbe esistere, perché in realtà per essere certi dell’esistenza
del limite bisognerebbe, in base ad un teorema, verificare che la funzione
![]() tende a quel
limite uniformemente al variare di
tende a quel
limite uniformemente al variare di ![]() tra 0 e
tra 0 e ![]() e che, in genere, si verifica utilizzando
la definizione di limite. Per evitare tale verifica laboriosa, possiamo più
semplicemente stabilire l’esistenza del limite trovato della funzione in
coordinate polari calcolando il limite della funzione f(x,y)
lungo una qualsiasi curva per Po, se questo però risulta diverso
allora non esiste il limite.
e che, in genere, si verifica utilizzando
la definizione di limite. Per evitare tale verifica laboriosa, possiamo più
semplicemente stabilire l’esistenza del limite trovato della funzione in
coordinate polari calcolando il limite della funzione f(x,y)
lungo una qualsiasi curva per Po, se questo però risulta diverso
allora non esiste il limite.
Esercizi guidati

Essendo diversi i limiti calcolati, si conclude che non esiste il limite della funzione data.
v Calcolo di limiti
Il limite:
![]()
è un limite doppio, perché si ottiene facendo tendere le due variabili x e y simultaneamente e indipendentemente rispettivamente a xo e yo . Ciò vuol dire che non bisogna calcolare tale limite facendo tendere dapprima la x a xo, considerando y costante, e successivamente facendo tendere, nella funzione così ottenuta nella sola variabile y, la y a yo, ossia:
![]()
Osservazioni:
Ø Se il
limite di f(x,y) dipende solo dalla variabile x o
solo dalla variabile y, allora il limite della funzione per P(x,y)
che tende a Po(xo, yo) si può
ricondurre al calcolo del limite di una funzione di una variabile,
rispettivamente per ![]()
Ø Se invece P tende all’infinito non è possibile ridurre il limite da calcolare al limite di una funzione di una sola variabile
Esercizi guidati
