A volte il metodo dello studio del segno della f ‘(x) per la ricerca dei massimi, minimi e flessi orizzontali di una funzione può risultare complicato a causa delle difficoltà che si possano incontrare nella risoluzione della disequazione f ‘(x)>0, specialmente se di tipo goniometrica. In questi casi si può ricorrere ad un altro procedimento detto metodo delle derivate successive alla prima che si basa sulla seguente proposizione:

Sia f(x) una funzione definita in [a; b] ed ivi continua insieme alle sue derivate f ‘, f ’’, f ‘’’, …f ⁿ. Sia inoltre x_o un punto interno di [a; b] in cui :

f ‘(x_o) = f ’’(x_o) = f ‘’’(x_o) =  … = f ^n-1(x_o) = 0   e    f ⁿ(x_o) ≠ 0

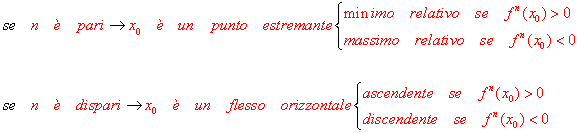
Quindi con tale metodo non si deve risolvere alcuna disequazione ma solo calcolare le derivate successive alla prima solo nel punto x₀ considerato. Una volta determinato gli zeri della f ‘(x) si calcola no le derivate successiva ad essa in tali zeri sino al momento in cui si trova un risultato diverso da zero . A tal fine guardiamo il seguente:

Esempio

Determinare i  punti estremanti e i punti di flesso a tangente orizzontale: