Premessa

Mi propongo, mediante esempi, di fornire le principali indicazioni finalizzate alla determinazione del campo di esistenza di una funzione numerica reale.

Quindi, data una funzione analitica , dobbiamo determinare il sottoinsieme I di R, i cui valori, attribuiti alla variabile indipendente x, non facciano perdere di significato alle operazioni che si devono eseguire per calcolare i corrispondenti valori    di y .

Premesso ciò, esamineremo via via le diverse funzioni analitiche, secondo la classificazione descritta precedentemente.

Ricerca del campo di esistenza di funzioni razionali

Tenendo presente quanto riportato nella lezione 3 : dominio , prendiamo in esame alcuni esempi di  funzioni razionali.

§ Campo di esistenza delle funzioni razionali intere

Determiniamo il C.E. delle seguenti funzioni:

§ :

§

§

Poiché figurano solo operazioni di addizione, moltiplicazione, divisione e potenza ad esponente un numero naturale, applicate sulla x,   le funzioni sono definite in tutto R, quindi scriveremo: C.E.:   o, anche,

§ Campo di esistenza delle funzioni razionali fratte

Determiniamo il campo di esistenza delle seguenti funzioni:

a)                         b)                          c)

      d)                 e)                      f)

Svolgimento:

a)

Per trovare il C.E. della f  dobbiamo individuare gli zeri del denominatore, ossia le soluzioni dell’equazione:                              

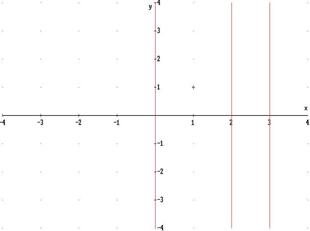
Poiché perla divisione perde di significato, basta escludere tale punto dall’insieme R per ottenere il campo di esistenza per cui scriveremo: C.E.:oppure. Il diagramma della funzione presenta dunque una discontinuità in x = 2 e a tal scopo tracceremo una retta (in rosso) parallela all’asse Y che separerà le curve componenti del grafico:

b)

Troviamo gli zeri del denominatore, ossia le soluzioni dell’equazione:

Quindi basta escludere tali punti dall’insieme R per ottenere il campo di esistenza per cui scriveremo: C.E.: oppure

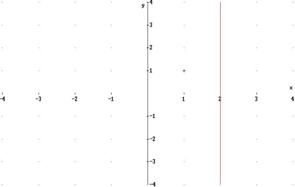
Il diagramma della funzione presenta, quindi, in x = 4 e x = -4 due punti di discontinuità, pertanto il grafico sarà costituito da tre curve separate dalle rette( in rosso)  x = 4 e x = -4:

c)

Troviamo gli zeri del denominatore, ossia dell’equazione:

,

poiché è impossibile che il quadrato di un numero reale sia uguale a un numero negativo si ha che:

quindi C.E. :.

d)

Troviamo gli zeri del denominatore, ossia dell’equazione:

essendo:

l’equazione non ammette soluzioni reali, quindi il denominatore non si annulla , pertanto C.E.: .

e)

Troviamo gli zeri del denominatore, ossia dell’equazione:

ricordando che una potenza, qualunque sia il suo esponente, è uguale a zero quando è nulla  la sua base si ha:

che è una soluzione doppia, essendo l’equazione di 2° grado, e che avremmo potuto calcolare anche applicando la formula risolutiva delle equazioni di secondo grado.

Dunque C.E.:.

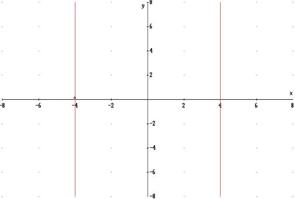
Graficamente:

f)

Troviamo gli zeri del denominatore, ossia dell’equazione:

calcoliamo ora le soluzioni dell’equazione di 2° grado o applicando la formula risolutiva o scomponendo il trinomio caratteristico a I membro in:

quindi, gli zeri del denominatore da escludere sono : 0, 2 e 3, pertanto C.E.:, oppure .

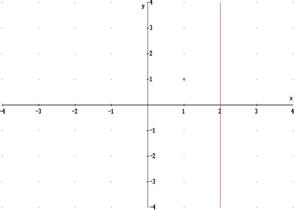
Graficamente: