In generale, le funzioni razionali fratte y = Aⁿ (x) / B^m (x):

§ hanno come campo di esistenza R escluso gli eventuali zeri del  denominatore

§ hanno tanti asintoti verticali quanti sono gli zeri del denominatore, eccetto nel caso sporadico in cui la funzione presenti una discontinuità eliminabile in uno di questi zeri

§ intersecano l’asse x nei punti in cui si annulla il numeratore

§ se n = m, hanno un asintoto orizzontale : y = a/b, rapporto dei coefficienti dei termini di maggior grado di  Aⁿ (x) e di B^m (x)

§ se n < m, hanno come asintoto orizzontale l’asse x, cioè y = 0

§ se n = m + 1, hanno un asintoto obliquo.

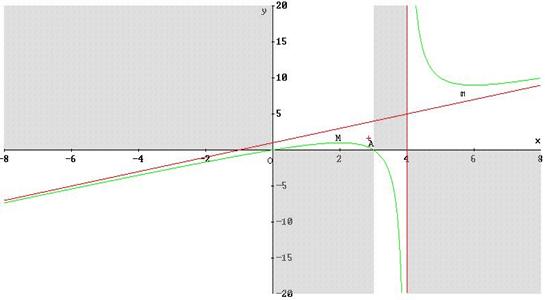
Studiamo e rappresentiamo graficamente la funzione:

Riportiamo le informazioni trovate nel piano cartesiano:

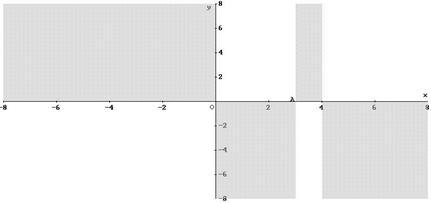
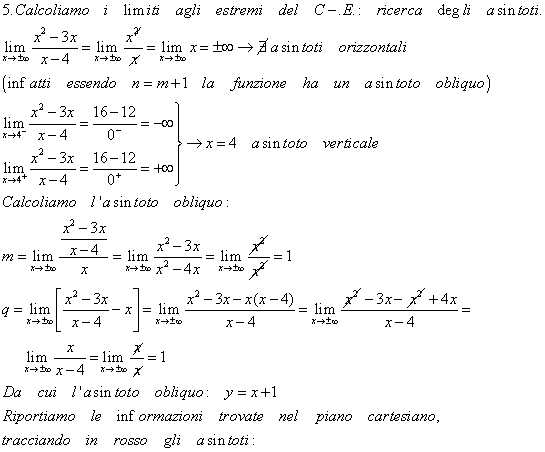
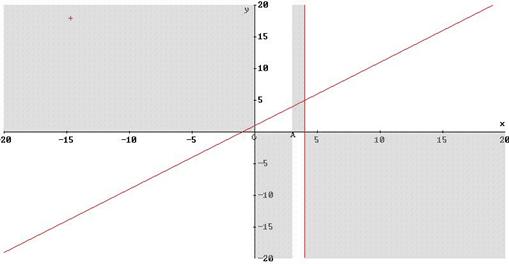
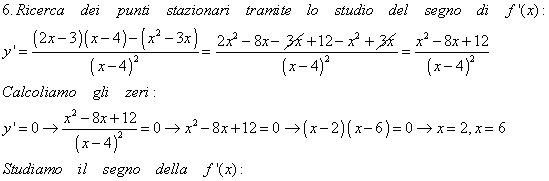
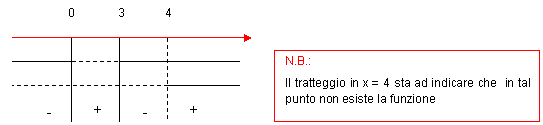
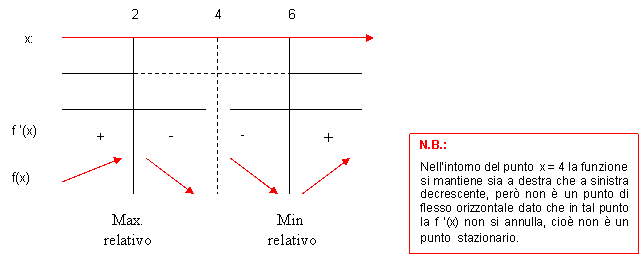
Si deduce che la curva ammette un massimo relativo in x = 2 e un minimo relativo in x = 6.

Calcoliamo le ordinate di tali punti:

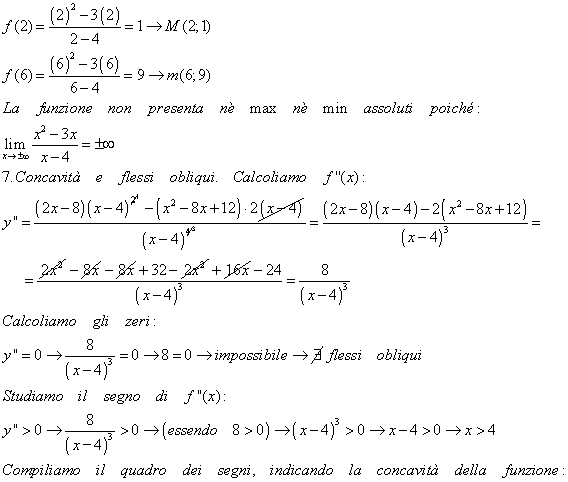
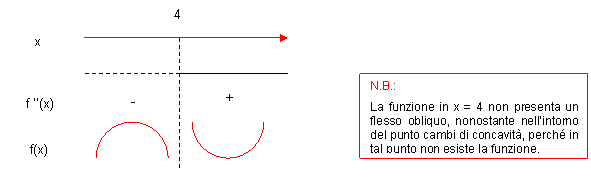
Riportiamo le informazioni trovate nel piano cartesiano e tracciamo il grafico della funzione: