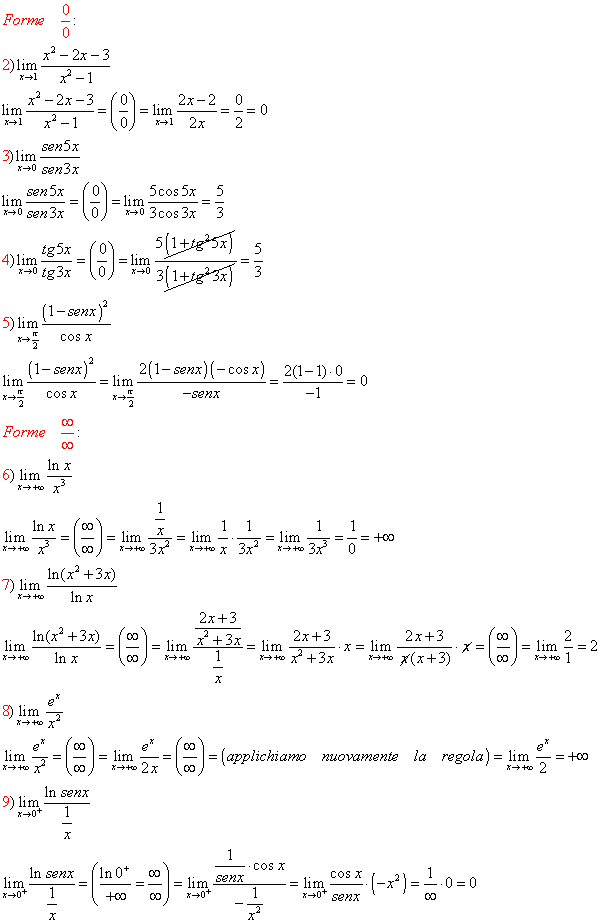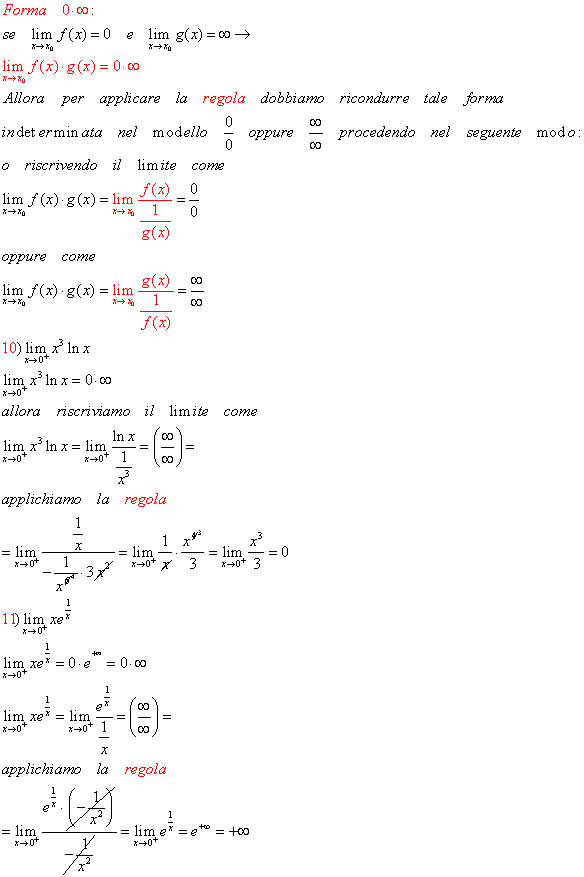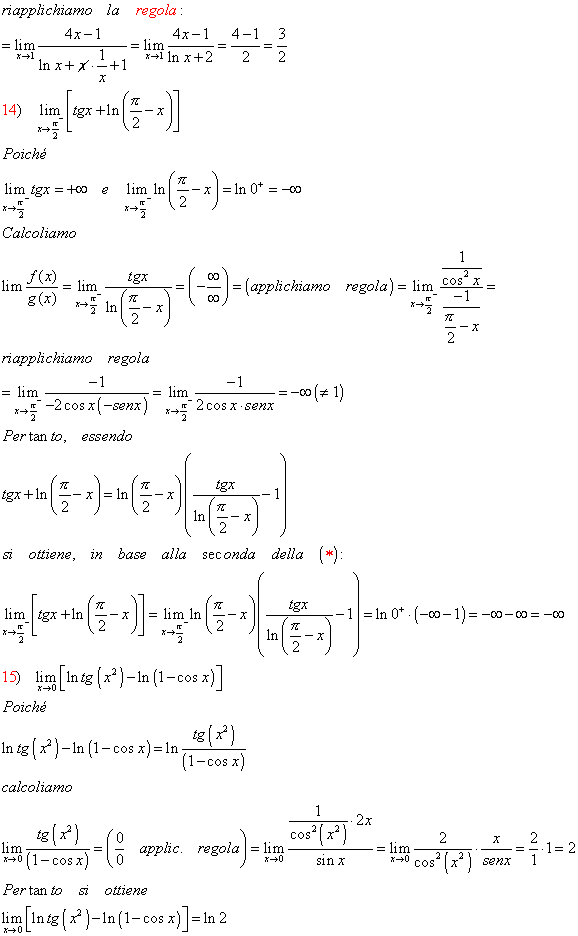Il 1° e il 2° teorema di De L’Hospital ci suggeriscono una regola pratica per calcolare i limiti di funzioni che si presentano nelle forme indeterminate:

agevolando notevolmente il calcolo di limiti di  altre forme indeterminate, come vedremo in seguito.I due teoremi di De l’Hospital si possono sintetizzare in un’unica proposizione detta Regola di De L’Hospital che possiamo così enunciare:

non confondere il rapporto delle derivate con la derivata del rapporto

Vediamo, adesso, attraverso degli esercizi come calcolare i limiti della seguenti funzioni che si   presentano nelle forme indeterminate (*) ed in altre ad esse riconducibili, del tipo 0⁰, 1^∞, ∞⁰ , applicando la Regola di De L’Hospital.

ESERCIZI GUIDATI

Solo nel primo esercizio esamineremo prima di applicare la regola di De l’Hospital se sono verificate tutte le ipotesi del teorema, al fine di comprenderne meglio il significato; dopodiché applicheremo direttamente la regola, perché le ipotesi saranno sicuramente valide se esiste il limite del rapporto delle derivate.