Teorema di Fermat: Se la funzione  f(x), definita in (a, b), possiede un massimo o un  minimo relativo nel punto x₀, interno all’intervallo (a;b), e derivabile in x₀ allora:

f ’(x₀) = 0

Geometricamente, il teorema significa che se una funzione ammette in un punto x₀ interno all’intervallo di definizione un massimo M o un minimo relativo m ed in tale punto esiste la retta tangente alla sua curva (essendo per ipotesi derivabile in x₀), allora tale tangente è parallela all’asse delle ascisse, ovvero il suo coefficiente angolare è 0. Vedi figure seguenti:

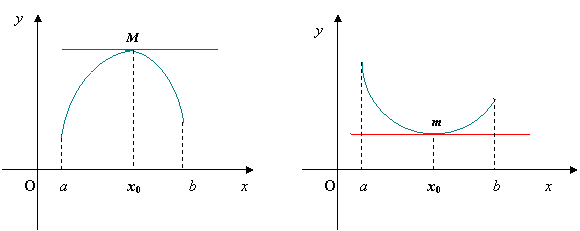
Teorema di Rolle: Se la funzione  f(x) soddisfa le seguenti ipotesi:

a) è continua nell’intervallo chiuso e limitato [a, b]

b) è derivabile nell’intervallo aperto (a, b)

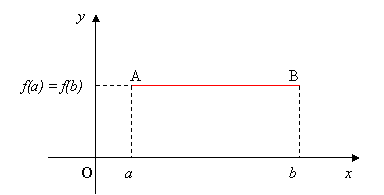
c) assume lo stesso valore negli estremi dell’intervallo di definizione, ovvero f(a) = f(b)

allora esiste almeno un punto c, interno all’intervallo (a, b),  in cui

f ’(c) = 0

Geometricamente, significa che, sotto le ipotesi di validità del teorema, esiste sull’arco AB della curva della funzione almeno un punto c in cui la retta tangente ( f ’(x) = 0 equivale m_t = 0) è parallela alla corda AB, e quindi all’asse delle ascisse. Vedi figura seguente:

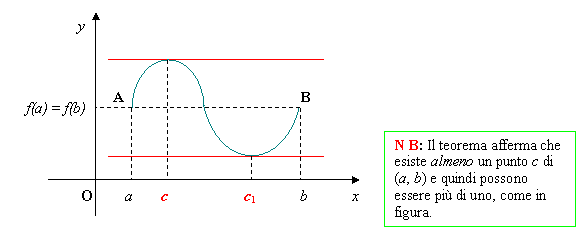
Conseguenze - Dal teorema di Rolle derivano i seguenti corollari:

1. Corollario: Se una funzione f(x) è

a) continua in [a, b]

b) derivabile in (a, b)

c) f ‘(x) = 0 in ogni punto interno dell’intervallo

  allora f(x) è costante in tutto [a,b].

2. Corollario: Se f(x) e g(x) sono due funzioni

a) continue nell’intervallo [a, b]

b) derivabili in (a, b)

c) f ‘(x) = g ‘(x) 

                         allora esse differiscono per una costante, cioè   f(x) - g(x) = k

Dimostrazione

Infatti, posto                                              z(x) = f(x) - g(x)  

si ha che                                  

z’(x) =  f ‘(x) – g‘(x) = 0 ( essendo per ipotesi f ‘(x) = g ‘(x) )  →  ( per il corollario 1.)  z (x) =  k

ESERCIZI GUIDATI

Teorema di Lagrange: Se una funzione f(x) è

a) continua in [a, b]

b) derivabile in (a, b)

                                        allora esiste almeno un punto c interno all’intervallo (a, b) in cui

Osservazione: il teorema di Lagrange è la generalizzazione del teorema di Rolle, infatti se

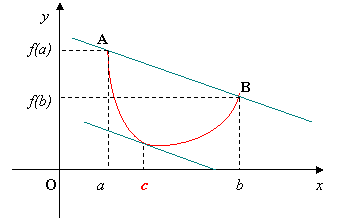
Geometricamente, significa che, sotto le ipotesi di validità del teorema, esiste sull’arco AB della curva almeno un punto c in cui la retta tangente (m_t equivale a f ‘(c)) è parallela alla corda AB

Ossia, esiste un punto interno all’intervallo in cui la rapidità istantanea di variazione (o derivata) della funzione risulta uguale alla rapidità media della funzione stessa nell’intervallo-.

Vedi figura seguente:

Conseguenze: dal teorema di Lagrange deriva il seguente corollario molto importante per lo studio di funzioni:

Corollario: Sia f(x) una funzione che soddisfa le ipotesi del teorema di Lagrange:

a) se f‘(x) è crescente in [a, b]

b) se f‘(x) è decrescente in [a, b]

Premetto che quando parliamo di funzioni crescenti o decrescenti senza precisare altro, intendiamo considerare funzioni crescenti o decrescenti  in senso stretto. Ciò significa che dobbiamo considerare la relazione < oppure > e non  ≥  oppure  ≤ , che invece si considerano per le funzioni crescenti o decrescenti in senso lato  che definiremo in seguito.

§ Una funzione f(x) è crescente in un intervallo se e solo se al crescere delle ascisse crescono le corrispondenti ordinate, ossia se:

Quindi nelle funzioni crescenti ad incrementi positivi (∆x) della x corrispondono incrementi (∆y) della y dello stesso segno e quindi positivi, ovvero i rapporti incrementali  ∆y/∆x sono sempre positivi.

Osserviamo attentamente il diagramma di due funzioni crescenti (in senso stretto):

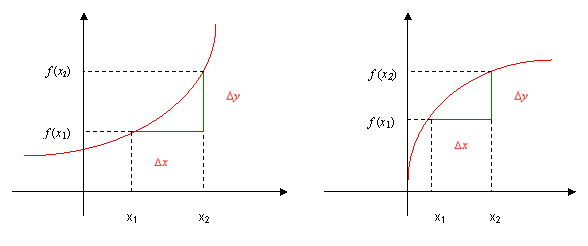
fig. 1a)                                                                                     fig. 1b)

§ Una funzione f(x) è decrescente in un intervallo se e solo se al crescere delle ascisse decrescono le corrispondenti ordinate, ossia se:

Pertanto nelle funzioni decrescenti ad incrementi (∆x) della x corrispondono decrementi (∆y)  della y, quindi i rapporti incrementali sono sempre negativi

Osserviamo attentamente i diagrammi di due funzioni decrescenti in senso stretto:

fig. 2a)                                                                                       fig. 2b)

Ebbene, se una funzione continua e derivabile ha derivata f ’(x) > 0  in tutti i punti dell’intervallo (aperto o chiuso) di definizione ciò comporta, per definizione di derivata, che il limite del rapporto incrementale è positivo e, per il teorema della permanenza del segno, che anche il rapporto incrementale è positivo, che come sappiamo è una caratteristica delle funzioni crescenti. 

Pertanto, possiamo dire che:

1. se risulta  f ’(x) > 0  in tutti i punti di [a;b]  allora la funzione è crescente in [a;b]

Invece, se una funzione continua e derivabile ha derivata f ’(x) < 0  in tutti i punti dell’intervallo (aperto o chiuso) di definizione ciò comporta, per definizione di derivata, che il limite del rapporto incrementale è negativo e, per il teorema della permanenza del segno, che anche il rapporto incrementale è negativo, che come sappiamo è una caratteristica delle funzioni crescenti. 

Pertanto, possiamo dire che:

2. se risulta  f ’(x) < 0  in tutti i punti di [a;b]  allora la funzione è decrescente in [a;b]

Non è vero il viceversa , ossia:

se la funzione è crescente (oppure decrescente) in [a;b] allora non è detto che sia f ’(x) > 0 (oppure  f ‘ (x) < 0 )

Infatti basta considerare come esempio il diagramma delle funzioni rappresentate in fig. 3a) e fig. 3b):

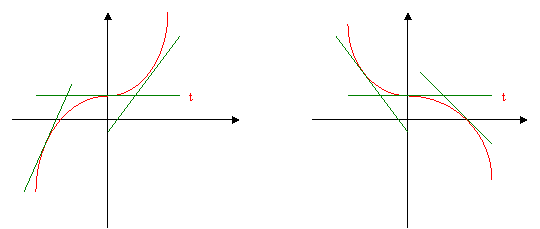
               fig. 3a)                                                                                 fig. 3b)

Infatti, come si osserva in fig. 3a) le tangenti ad una curva con andamento strettamente crescente  o hanno coefficiente angolare m >0 (perché formano con l’asse delle x un angolo acuto) oppure m = 0 (perché la retta tangente t è parallela all’asse delle x) e pertanto, tenuto conto dell’interpretazione geometrica della derivata prima di una funzione in un punto x generico dell’intervallo di definizione, si ha dunque che in tali punti risultano rispettivamente f ’(x) > 0 oppure  f ’(x) = 0.

Analogamente, dal grafico illustrato in fig.3b) si rileva che se  la funzione  ha andamento decrescente la condizione f ’(x) < 0 non risulta verificata in tutti i punti x interni all’intervallo di definizione. Infatti la tangente t nel punto x = 0 ha coefficiente angolare m = 0 e quindi f ’(x) = 0.

Pertanto, possiamo affermare che:

se f (x) è crescente (o decrescente) → f ’(x) ≥ 0  ( o f ’(x) ≤ 0 )

Come vedremo meglio in seguito, il punto nell’intorno del quale la funzione è sempre crescente (o sempre decrescente) e con derivata prima nulla viene denominato flesso a tangente orizzontale (vedi fig. 3 a) e fig. 3b)).

Come è stata definita la funzione crescente e decrescente nell’intervallo [a;b], cioè globalmente, allo stesso modo si definisce la funzione crescente e decrescente in un punto x_o interno ad [a;b]. Solo che questa volta non si tratta di una proprietà globale ma di una proprietà locale della f(x), ossia di una proprietà valida soltanto in un opportuno intorno del punto x_o.

Infatti, una funzione si dice crescente o decrescente nel punto x_o se e soltanto se in un intorno completo di x_o, (x_o - h ; x_o + h) contenuto in [a; b], si verificano rispettivamente le seguenti implicazioni:

se x_o - h < x_o < x_o + h →  f(x_o – h) < f(x_o) < f(x_o + h)

oppure

se   x_o - h < x_o < x_o + h → f(x_o – h) > f(x_o) > f(x_o + h)

Osservazione

Per determinare, dunque, gli intervalli in cui una funzione è crescente o decrescente basta studiare il segno della sua derivata prima.

Esempio

Determinare in quali intervalli è crescente o decrescente la seguente funzione

y = x³- 3 x ² + 1

Innanzitutto determiniamo il dominio: la funzione è definita per ogni x reale.

Per determinare in quali intervalli la f(x) è crescente o decrescente studiamo il segno della sua derivata prima che è la seguente:

y ‘ = 3 x² - 6 x

Studiamo y’ > 0:

3 x² -6 x > 0 →  x² -2 x > 0 → x(x -2) > 0 → ( x = 0 , x = 2) →  x < 0 V x > 2

Compiliamo il quadro dei segni:

In corrispondenza degli intervalli con segno positivo, tracciamo la freccia rivolta verso l’alto per indicare che la funzione è crescente; in corrispondenza di quelli con segno negativo tracciamo la freccia rivolta verso il basso per indicare che la funzione è decrescente

Quindi la funzione è crescente per x < 0 V x > 2 mentre è decrescente nel restante intervallo, cioè per 0 < x < 2.

ESERCIZIO GUIDATO

Teorema di Cauchy: Se f(x) e g(x) sono due funzioni

a) continue nell’intervallo [a, b]

b) derivabili in (a, b) e

                                    allora esiste almeno un punto c interno ad (a, b) tale che

ovvero il rapporto fra le derivate delle due funzioni calcolate in un particolare punto c interno ad (a, b) è uguale al rapporto fra i rispettivi incrementi nell’intervallo [a, b].

Osservazione: il teorema di Cauchy è la generalizzazione del teorema di Lagrange, infatti se

Teorema (Regola) di De L’Hospital: Se due funzioni f(x) e g(x) soddisfano le seguenti ipotesi:

a)  o

b) f(x) e g(x) sono derivabili in un intorno di x₀ e in tale intorno g’(x) ≠ 0

c) esiste il seguente limite:

                                                                 allora si ha:

Il teorema consente di risolvere le forme indeterminate del tipo:

Inoltre il teorema sussiste anche nel caso in cui  x  tende ad infinito anziché a x_o.

Osservazione: la regola di De Hospital può essere applicata solo quando esiste il limite del rapporto delle derivate. Tuttavia nel calcolo di un limite, anche se formalmente è impreciso, diamo per certa l’esistenza di tale limite: sarà il risultato finale a giustificare l’esattezza dello svolgimento.

Vengono elencati qui di seguito alcuni accorgimenti per ricondurre una qualsiasi forma indeterminata ad una forma dove si possa applicare la regola di De Hospital:

1. Forma indeterminata del tipo 0 ^. ∞: si riconduce a uno dei precedenti casi   indeterminati

mediante la trasformazione:

2. Forme indeterminate tipo 0^o, ∞^o, 1^∞: il limite da calcolare è della forma  f(x)^g(x) che si 

riconduce alle precedenti forme indeterminate 

                                                                    mediante la trasformazione:

3. Forma indeterminata ∞ - ∞: se esiste    allora si può ricondurre a uno  dei

precedenti casi indeterminati con la trasformazione:

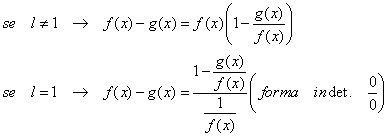
Vedi:

§ relative applicazioni guidate nella lezione  Regola di De L’Hospital

§ suo utilizzo anche nel  Confronto tra infiniti o infinitesimi