Per affrontare lo studio di funzioni di due variabili è necessario introdurre alcuni concetti di topologia relativi ai punti del piano analoghi a quelli introdotti per le funzioni di una variabile relativi però ai punti di una retta.

Intorni

v Si definisce intorno circolare di un punto P_o(x_o,y_o) del piano l’insieme dei punti del piano le cui coordinate (x,y) soddisfano la disequazione:

(x- x_o)² + (y - y_o)² < r²

con r un numero reale positivo.

Esempio: l’insieme

rappresenta un intorno circolare di centro P(0,0) e raggio r = 2.

Graficamente, l’intorno circolare è rappresentato dai punti interni del cerchio di centro P_o(x_o,y_o)  e raggio r  e quindi possiamo anche dire intorno circolare di centro P e raggio r:

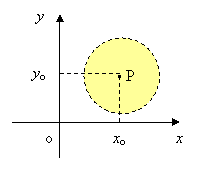
v Si definisce intorno di infinito l’insieme dei punti del piano le cui coordinate (x,y) soddisfano la disequazione:

(x- x_o)² + (y - y_o)² > r²

con r un numero reale positivo.

Esempio: l’insieme

rappresenta un intorno infinito di centro P(3,2) e raggio r = 1.

Graficamente, l’intorno circolare è rappresentato dai punti esterni del cerchio di centro P(x_o,y_o) e raggio r grande quanto si vuole:

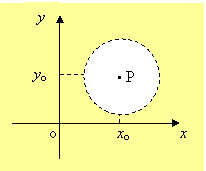
v Si definisce intorno di un punto P_o(x_o,y_o) del piano ogni sottoinsieme di R² che contiene un intorno circolare di centro P_o:

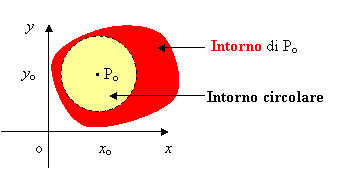
Punti

v Si dice che P_o(x_o,y_o) è un punto di accumulazione per l’insieme I dei punti del piano se comunque fissato un intorno circolare di centro P_o esso contiene infiniti punti di I.

Esempio: l’insieme:

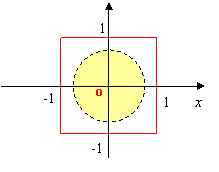
     Il punto O(0, 0) è di accumulazione per I, in quanto preso un qualunque intorno circolare di centro O e raggio r<1 in esso cadono infiniti punti di I.

v Si dice che P_o(x_o,y_o) è un punto di frontiera per l’insieme I dei punti del piano se ogni intorno circolare di centro P_o ha punti che appartengono a I e punti che non appartengono a I

Esempio:riprendendo l’insieme I dell’esempio precedente, vedi figura:

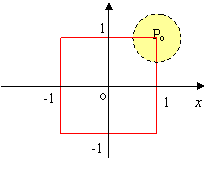
puoi osservare che un qualunque punto preso solo sui lati del quadrato (in rosso), ad esempio P_o(1,1) è di frontiera per I, perché in ogni suo intorno circolare o  cadono punti di I o non ne cadono.

v L’insieme dei punti di frontiera di un insieme I è detto frontiera

v Si dice che P_o(x_o,y_o) è un punto interno all’insieme I dei punti del piano se esiste un intorno di P_o che contiene soltanto punti di I

v Si dice che P_o(x_o,y_o) è un punto esterno all’insieme I dei punti del piano se esiste un intorno di P_o che non contiene alcun punto di I

Riepilogando:

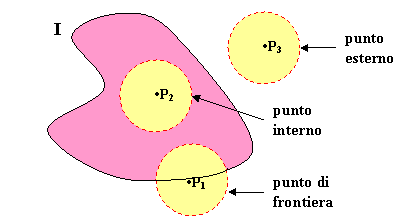
Come puoi osservare dalla figura il punto di frontiera e il punto interno sono punti di accumulazione.

Insiemi

Dato un insieme I di punti del piano si dice:

v Insieme chiuso se contiene tutti i punti della sua frontiera

v Insieme aperto se non contiene alcun punto della sua frontiera

Ad esempio, un poligono è un insieme di punti chiuso però, se lo priviamo dei punti dei suoi lati diventa un insieme aperto.

v Insieme limitato se esiste un intorno di un qualsiasi punto che contiene tutti i punti di I, altrimenti è illimitato

Ad esempio, l’insieme dei punti di un poligono è limitato, mentre l’insieme dei punti di un angolo è illimitato.

Esercizi guidati

1. Stabilire se l’insieme  è un intorno circolare del punto P(0,1).

Come si osserva:   x² + y² = 4  rappresenta nel piano Oxy una circonferenza di centro O(0,0) e raggio r =2, pertanto i punti (x,y) di I soddisfacenti la disequazione  x² + y² < 4   rappresentano un intorno circolare di O e non di P

2. Stabilire se l’insieme  è un intorno del punto P(1,0).

Rappresentando nel piano Oxy l’insieme I:

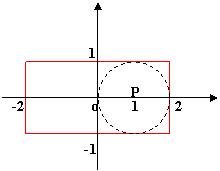
Come osservi dal grafico, l’insieme I, rappresentato dal rettangolo, è un intorno del punto P perché contiene come intorno circolare di centro P il cerchio di centro P e raggio r = 1

3. Stabilire se:

· P(1,0) è un punto di accumulazione per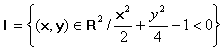

· P è un punto esterno, interno o di frontiera

· l’insieme I è chiuso o aperto, limitato o illimitato

L’equazione associata alla disequazione data rappresenta nel piano Oxy un’ellisse di centro O e semiassi lunghi 1 e 2:

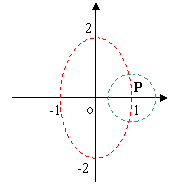
Come puoi osservare, dalla figura, P è un punto di accumulazione, perché qualunque semicerchio centrato in  P contiene infiniti punti di I.

P non è un punto né esterno né interno ma di frontiera, perché qualunque intorno di P contiene punti di I e punti non appartenenti ad I.

L’insieme I, rappresentato graficamente da tutti e soli i punti interni all’ellisse escluso, dunque, i punti dell’ellisse, è un insieme aperto perché non contiene alcun punto della frontiera.

L’insieme I è limitato perché possiamo considerare come intorno un qualsiasi sottoinsieme del piano che lo include nel suo interno: