Enunciamo il seguente

Terema della media: L’integrale definito di una funzione f(x), continua in [a; b], è uguale al

                                      prodotto dell’ampiezza dell’intervallo d’integrazione per il valore che

                                      la funzione f(x) assume in un particolare punto c dell’intervallo, ossia:

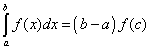
Geometricamente:

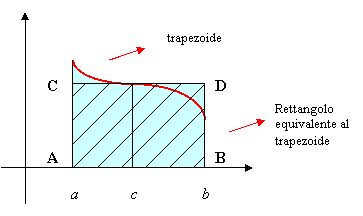
si può sempre costruire un opportuno rettangolo di base (b-a) ed  altezza dato dal valore f(c) che  f(x) assume in un  particolare punto c di [a; b] e pertanto di area (b-a) f(c), che risulta equivalente al trapezoide delimitato dal grafico della curva f(x) in [a; b] e la cui area è uguale all’integrale definito di f(x) da a a  b.

Però il teorema della media afferma l’esistenza del punto c ma non fornisce indicazioni su come calcolarlo. Tuttavia è possibile ricavare f(c) dall’uguaglianza e ottenere:

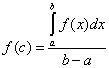
Il valore f(c) prende il nome di valore medio della funzione f(x). Infatti

Ciò giustifica la definizione data relativa al valor medio f(c) degli infiniti valori assunti dalla funzione f(x) al variare di x in [a; b].

Esempio

Calcolare il valore medio della funzione  y = x² , continua nell’intervallo [1; 5].