Un Diagramma di Wöhler è un grafico su base statistica che mette in relazione la componente alternata di un ciclo di fatica con il numero di cicli che un provino sopporta prima della rottura.
La sua costruzione del diagramma avviene in questo modo: si ricostruisce in laboratorio un determinato ciclo di sollecitazione con una determinata ampiezza e lo si applica ad un elevato numero di provini, annotando il numero di cicli che essi sopportano prima della rottura. Successivamente si ripete la stessa serie di esperimenti a diversi valori della sigma alternata (componente alternata del ciclo di sforzo).
Parametri ricavabili da una curva di Wöhler
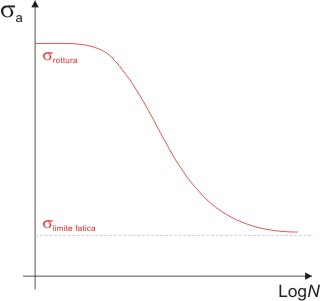
La curva di Wöhler non interseca l'asse delle ordinate (cioè per N = 1/2, in scala logaritmica) in corrispondenza anche di mezzo carico di rottura statico del materiale, avremo un valore infinito della resistenza a fatica che è fatale al pezzo. Successivamente si mantiene costante per un certo tratto, per poi decrescere piuttosto velocemente, in genere tra N = 10^3 N = 10^6.
Per molte leghe ferrose (ad esclusione quindi di alluminio, rame, magnesio), essa presenta poi una sorta di asintoto orizzontale che tende ad un valore dello sforzo detto limite di fatica: esso rappresenta il valore della σ al di sotto del quale, anche per un numero idealmente infinito di cicli, il materiale non si romperà per fatica. Si è soliti dividere il diagramma di Wöhler in due regioni, dette LCF (Low-Cycle Fatigue, fatica a basso numero di cicli) e HCF (High-Cycle Fatigue, fatica ad alto numero di cicli), la prima per valori di sigma superiori al carico di snervamento del materiale, dove si hanno plasticizzazioni macroscopiche e di conseguenza la vita del materiale è assai ridotta; la seconda per valori di sigma inferiori, dove le plasticizzazioni cicliche sussistono solo a livello microscopico.
L’effetto della temperatura è notevole. La resistenza a fatica diminuisce con l’aumentare della temperatura, ma la quantificazione di tale diminuzione dipende dallalega e dalla temperatura.